Estimating Policy Barriers to Trade
22 November 2019
Brendan Cooley
Ph.D. Candidate
Princeton University
bcooley (at) princeton.edu
Introduction
Free and Fair?
“We believe that trade must be fair and reciprocal. The United States will not be taken advantage of any longer.”
\(\qquad\) – Donald Trump, Feb. 2019
“I’m going to have a trade prosecutor…to make sure every trade deal we’re already in is absolutely followed to the letter so nobody takes advantage of us.”
\(\qquad\) – Hillary Clinton, Oct. 2016
“Internationally, we are seeing a tendency toward protectionism and navel-gazing…What we need is trade that’s both fair and free.”
\(\qquad\) – Shinzo Abe, Oct. 2016
“An open world is only worth it if the competition that takes place there is fair.”
\(\qquad\) – Emmanuel Macron, Sep. 2017
- Free: Foreign firms enjoy same market access conditions as domestic competitors
- Fair: Barriers that do exist affect all trade partners symmetrically
The Tariff System (GATT/WTO)
- Free? Applied tariff rates are low, ~5% on average (Baldwin 2016)
- Fair? WTO members (vast majority of world economy) commit to principle of non-discrimination (Most Favored Nation)
The Tariff System (GATT/WTO)
- Free? Applied tariff rates are low, ~5% on average (Baldwin 2016)
- Fair? WTO members (vast majority of world economy) commit to principle of non-discrimination (Most Favored Nation)
Varieties of Barriers
Direct
- Tariffs
- Non-Tariff Measures (NTMs)
- Price controls, quotas, health and safety regulations, technical barriers
- Mansfield and Busch (1995), Lee and Swagel (1997), Gawande and Hansen (1999), Kono (2006), Rickard (2012), Maggi, Mrázová, and Neary (2018)
Indirect (Behind-the-Border)
- Government procurement
- Evenett and Hoekman (2004), Kono and Rickard (2014)
- Subsidies
- Excise taxes
- Regulations
Effective Discrimination: Target trade-disorting instruments to disproportionately affect disfavored trading partners.
- E.g. high agricultural duties by developed countries disproportionately harm developing countries
Approach
Trade Costs: Policy distortions and transportation costs to access market \(i\) in excess of those faced by firms in country \(i\)
Overview
- Build model of international economy subject to trade costs (Eaton and Kortum 2002)
- Derive structural relationship linking trade costs to price levels, trade flows, market shares of home producers (observables)
- Anderson and Van Wincoop (2003), Waugh (2010), Simonovska and Waugh (2014), Sposi (2015), Waugh and Ravikumar (2016)
- Decompose trade costs into economic (transportation costs) and political (policy barriers) components
- Model transportation costs, combine with data on variables in (2) to separately estimate magnitude of policy barriers
\(\tau_{ij} - 1 \geq 0\) – ad valorem tariff equivalent of policy barriers gov \(i\) imposes on gov \(j\)
Estimand
\[ \bm{\tau}_{N \times N} = \begin{pmatrix} 1 & \cdots & \tau_{1n} \\ \vdots & \ddots & \vdots \\ \tau_{n1} & \cdots & 1 \end{pmatrix} \]
Measurement Matters
Measurement Matters
Model
Model (Overview)
- \(\bm{d}_{N \times N} = \bm{\delta} \circ \bm{\tau}\) - trade costs (economic and political)
\[ \bm{d}_{N \times N} \mapsto \left( \bm{X}_{N \times N}, \bm{P}_{N \times 1} \right) \]
- \(\bm{X}_{N \times N}\) - trade flows
- \(\bm{P}_{N \times 1}\) - price levels
- Based on Eaton and Kortum (2002) (Ricardian model, technological differences as basis for trade, competitive economy)
- Equilibrium predictions isomorphic to models with market imperfections (e.g. Melitz 2003; Chaney 2008), see Head and Mayer (2014) and Costinot and Rodríguez-Clare (2015)
Model (Overview)
- \(\bm{d}_{N \times N} = \bm{\delta} \circ \bm{\tau}\) - trade costs (economic and political)
\[ \bm{d}_{N \times N} \mapsto \left( \color{bcOrange} \bm{X}_{N \times N}, \bm{P}_{N \times 1} \color{black} \right) \]
- \(\color{bcOrange} \bm{X}_{N \times N}\) - trade flows
- \(\color{bcOrange} \bm{P}_{N \times 1}\) - price levels
- Based on Eaton and Kortum (2002) (Ricardian model, technological differences as basis for trade, competitive economy)
- Equilibrium predictions isomorphic to models with market imperfections (e.g. Melitz 2003; Chaney 2008), see Head and Mayer (2014) and Costinot and Rodríguez-Clare (2015)
Observables
\[ \left( \color{bcOrange} \bm{X}_{N \times N}, \bm{P}_{N \times 1} \color{black} \right) \mapsto \bm{d}_{N \times N} \]
Consumption (I)
Consumer’s Problem
\[\begin{equation*} \label{eq:consumer} \begin{split} \max & \quad U_i = Q_i^{\nu_i} S_i^{1 - \nu_i} \\ \text{subject to} & \quad P_i Q_i + P_i^s S_i \leq w_i L_i \end{split} \end{equation*}\]
- \(Q_i\) - aggregate of tradable goods
- \(S_i\) - homogenous services
Tradable Goods
- Continuum of tradable goods indexed \(\omega \in \Omega = [0, 1]\)
- Set \(\mathcal{K}\) of good categories \[ h : \Omega \rightarrow \mathcal{K} \]
- \(\alpha_k\) relative preference for goods in category \(k\)
\[ Q_i = \left( \int_{[0,1]} \alpha_{h(\omega)}^{\frac{1}{\sigma}} q_i(\omega)^{\frac{\sigma - 1}{\sigma}} d \omega \right)^{\frac{\sigma}{\sigma - 1}} \]
Consumption (II)
Tradable Price Index
\[ P_i = \left( \int_{[0,1]} \alpha_{h(\omega)} p_i(\omega)^{1 - \sigma} d \omega \right)^{\frac{1}{1 - \sigma}} \]
Expenditure on Tradables
\[ E_i^q = \nu_i I_i + D_i = P_i Q_i^\star \]
Model (Production)
- Competitive international economy, every country can produce each variety \(\omega\)
“Fundamental” Cost
\[ c_i = w_i^{1 - \beta} P_i^{\beta} \]
- \(w_i\) - cost of labor
- \(P_i\) - cost of composite intermediate good
- equivalent to composite consumption good
Product-Specific Costs, Local Prices
- Technology shocks \(z_i(\omega)\) shift local prices
\[ p_{ii}(\omega) = \frac{c_i}{z_i(\omega)} \]
Technology (Fréchet) (Fréchet Distribution)
\[ F_i(z) = \text{Pr} \left\{ z_i(\omega) \leq z \right\} = \exp \left\{ - T_i z^{-\theta} \right\} \]
- \(T_i\) - “fundamental” productivity
Prices and Trade Costs
Prices and Trade Costs
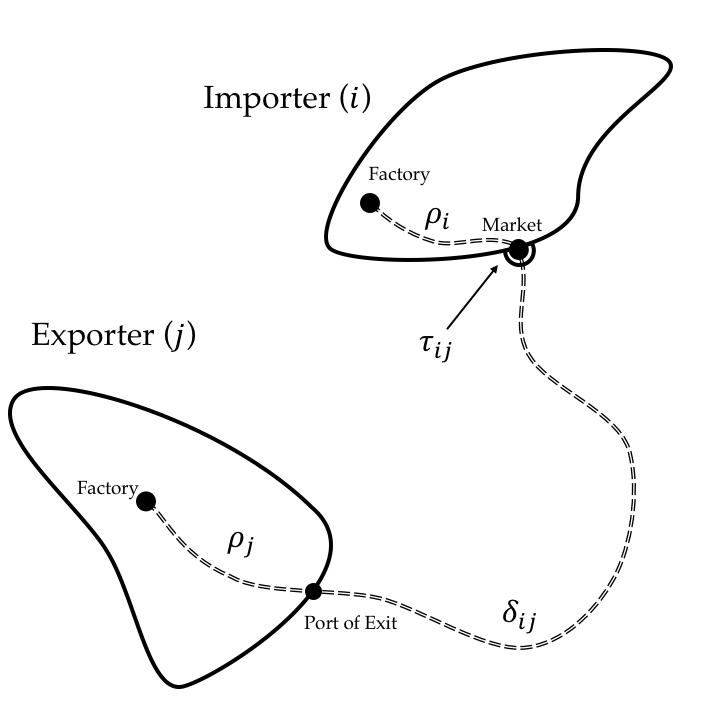
\[ p_{ji}(\omega) = d_{ji} p_{ii}(\omega) \]
\[ d_{ij} = \rho_j \delta_{ij} \tau_{ij} \]
- \(\tau_{ij} = 1 \implies\) no policy distortion
- \(\tau_{jj} = \delta_{jj} = 1\)
\[ p_i^\star(\omega) = \min_{j \in \left\{ 1,...,N \right\}} \left\{ p_{ij} \right\} \]
\[ \Omega_{ij}^\star = \left\{ \omega \in [0,1] \text{ } \bigg| \text{ } p_{ij}(\omega) \leq \min_{k \neq j} \left\{ p_{ik} \right\} \right\} \]
Equilibrium
Prices
\[ P_i(\bm{w}) = \left( \int_{\omega \in [0,1]} \alpha_{h(\omega)} p_i^\star(\omega)^{1 - \sigma} d \omega \right)^{\frac{1}{1 - \sigma}} \]
Trade Flows
\[ X_{ij}(\bm{w}) = \int_{\color{bcOrange} \omega \in \Omega_{ij}^\star \color{black}} p_{ij}(\omega) \tilde{q}_i \left( p_{ij} (\omega) \right) d \omega \]
- \(\tilde{q}_i \left( p_{ij} (\omega) \right)\) - consumer and producer demand for good \(\omega\)
Market Clearing
\[\begin{equation} \underbrace{\sum_{j} X_{ji}(\bm{w})}_{\text{tradable sales}} + D_i = \underbrace{\sum_j X_{ij}(\bm{w})}_{\text{tradable expenditure}} \label{eq:marketClearing} \end{equation}\]
Definition: An international equilibrium is a vector of wages \(\bm{w}\) such that (\(\ref{eq:marketClearing}\)) holds for each country.
- Alvarez and Lucas (2007): existence and uniqueness
Identification (I)
- \(\lambda_{ij} = \frac{X_{ij}}{E_i}\) - share of \(i\)’s tradable expenditure spent on goods from \(j\)
Gravity Equation
\[ \lambda_{ij} = \frac{ T_j \left( \color{bcOrange} d_{ij} \color{black} w_j^{1 - \beta} P_j^{\beta} \right)^{- \theta} }{\gamma^{-1} P_i^{-\theta}} \]
- \(\color{bcOrange} d_{ij} \color{black} = \rho_j \delta_{ij} \tau_{ij}\)
Origin Differences
\[ \frac{\lambda_{ij}}{\lambda_{jj}} = \left( \delta_{ij} \tau_{ij} \frac{P_j}{P_i} \right)^{-\theta} \]
Identification (II)
Origin Differences
\[ \frac{\lambda_{ij}}{\lambda_{jj}} = \left( \delta_{ij} \tau_{ij} \frac{P_j}{P_i} \right)^{-\theta} \]
Rationales for Divergence (\(\frac{\lambda_{ij}}{\lambda_{jj}} < 1\))
Identification (II)
Origin Differences
\[ \frac{\lambda_{ij}}{\lambda_{jj}} = \left( \delta_{ij} \tau_{ij} \color{bcOrange} \frac{P_j}{P_i} \color{black} \right)^{-\theta} \]
Rationales for Divergence (\(\frac{\lambda_{ij}}{\lambda_{jj}} < 1\))
- Price differences, \(\color{bcOrange} P_j < P_i\)
Identification (II)
Origin Differences
\[ \frac{\lambda_{ij}}{\lambda_{jj}} = \left( \color{bcOrange} \delta_{ij} \tau_{ij} \color{black} \frac{P_j}{P_i} \right)^{-\theta} \]
Rationales for Divergence (\(\frac{\lambda_{ij}}{\lambda_{jj}} < 1\))
- Price differences, \(P_j < P_i\)
- Trade costs \(\color{bcOrange} \delta_{ij} \tau_{ij} > 1\)
Inversion
\[ \tau_{ij} = \left( \frac{\lambda_{ij}}{\lambda_{jj}} \right)^{-\frac{1}{\theta}} \frac{P_i}{P_j} \frac{1}{\delta_{ij}} \]
Data
Data and Measurement
\[ \tau_{ij} = \left( \frac{\lambda_{ij}}{\lambda_{jj}} \right)^{-\frac{1}{\theta}} \frac{P_i}{P_j} \frac{1}{\delta_{ij}} \]
Data and Measurement
\[ \tau_{ij} = \left( \color{bcOrange} \frac{\lambda_{ij}}{\lambda_{jj}} \color{black} \right)^{-\frac{1}{\theta}} \frac{P_i}{P_j} \frac{1}{\delta_{ij}} \]
- \(\color{bcOrange} \frac{\lambda_{ij}}{\lambda_{jj}}\) - relative expenditure shares
- Data: trade flows and national accounts
Data and Measurement
\[ \tau_{ij} = \left( \frac{\lambda_{ij}}{\lambda_{jj}} \right)^{-\frac{1}{\theta}} \color{bcOrange} \frac{P_i}{P_j} \color{black} \frac{1}{\delta_{ij}} \]
- \(\frac{\lambda_{ij}}{\lambda_{jj}}\) - relative expenditure shares
- Data: trade flows and national accounts
- \(\color{bcOrange} \frac{P_i}{P_j}\) - relative price levels
- Data: International Comparison Program (World Bank), good prices and exchange rates
- Estimate preference weights, \(\bm{\alpha}\)
Data and Measurement
\[ \tau_{ij} = \left( \frac{\lambda_{ij}}{\lambda_{jj}} \right)^{-\frac{1}{\theta}} \frac{P_i}{P_j} \color{bcOrange} \frac{1}{\delta_{ij}} \]
- \(\frac{\lambda_{ij}}{\lambda_{jj}}\) - relative expenditure shares
- Data: trade flows and national accounts
- \(\frac{P_i}{P_j}\) - relative price levels
- Data: International Comparison Program (World Bank), good prices and exchange rates
- Estimate preference weights, \(\bm{\alpha}\)
- \(\color{bcOrange} \delta_{ij}(\bm{Z}_{ij})\)
- \(\bm{Z}_{ij}\) dyadic geographic covariates
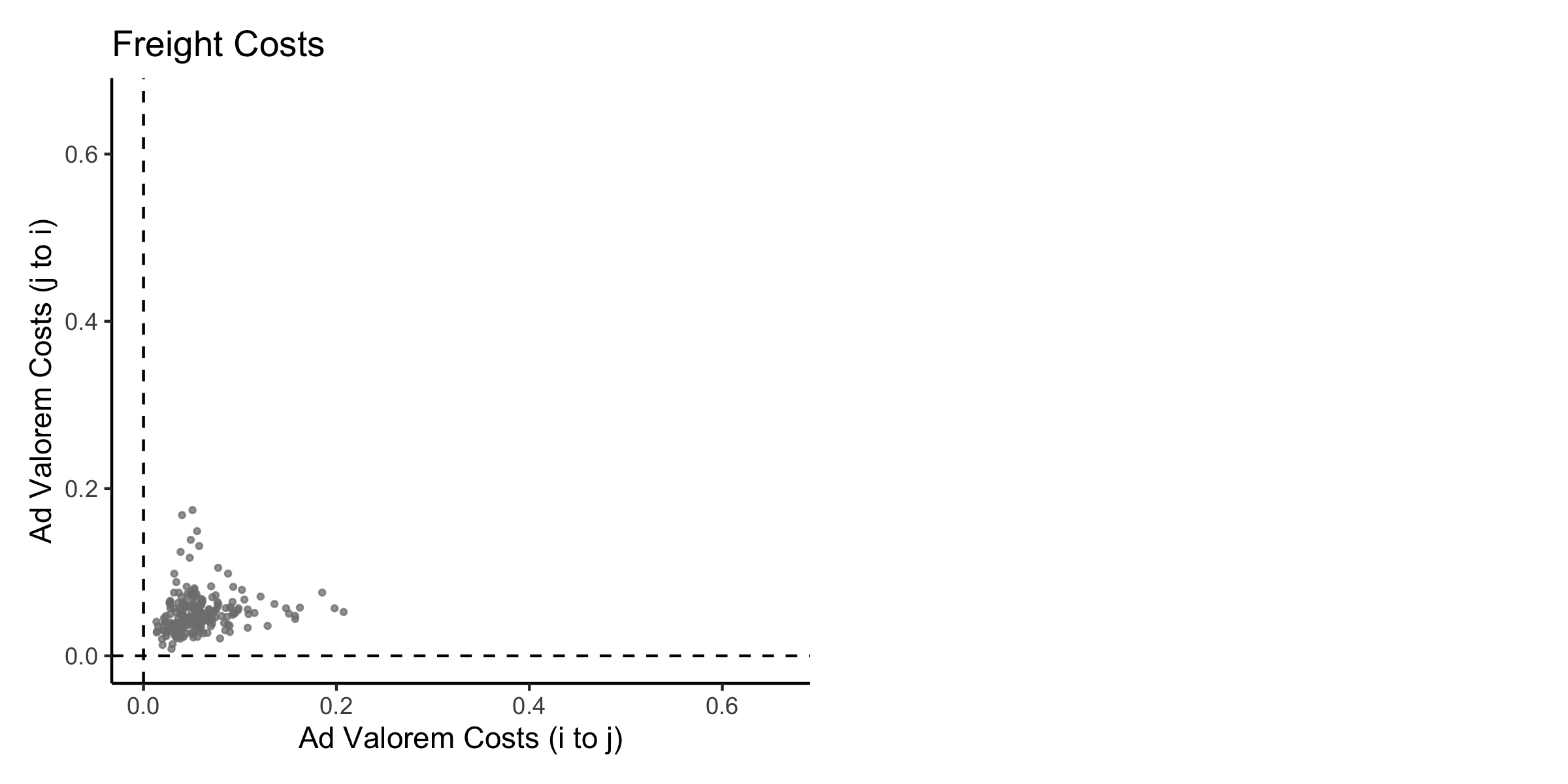
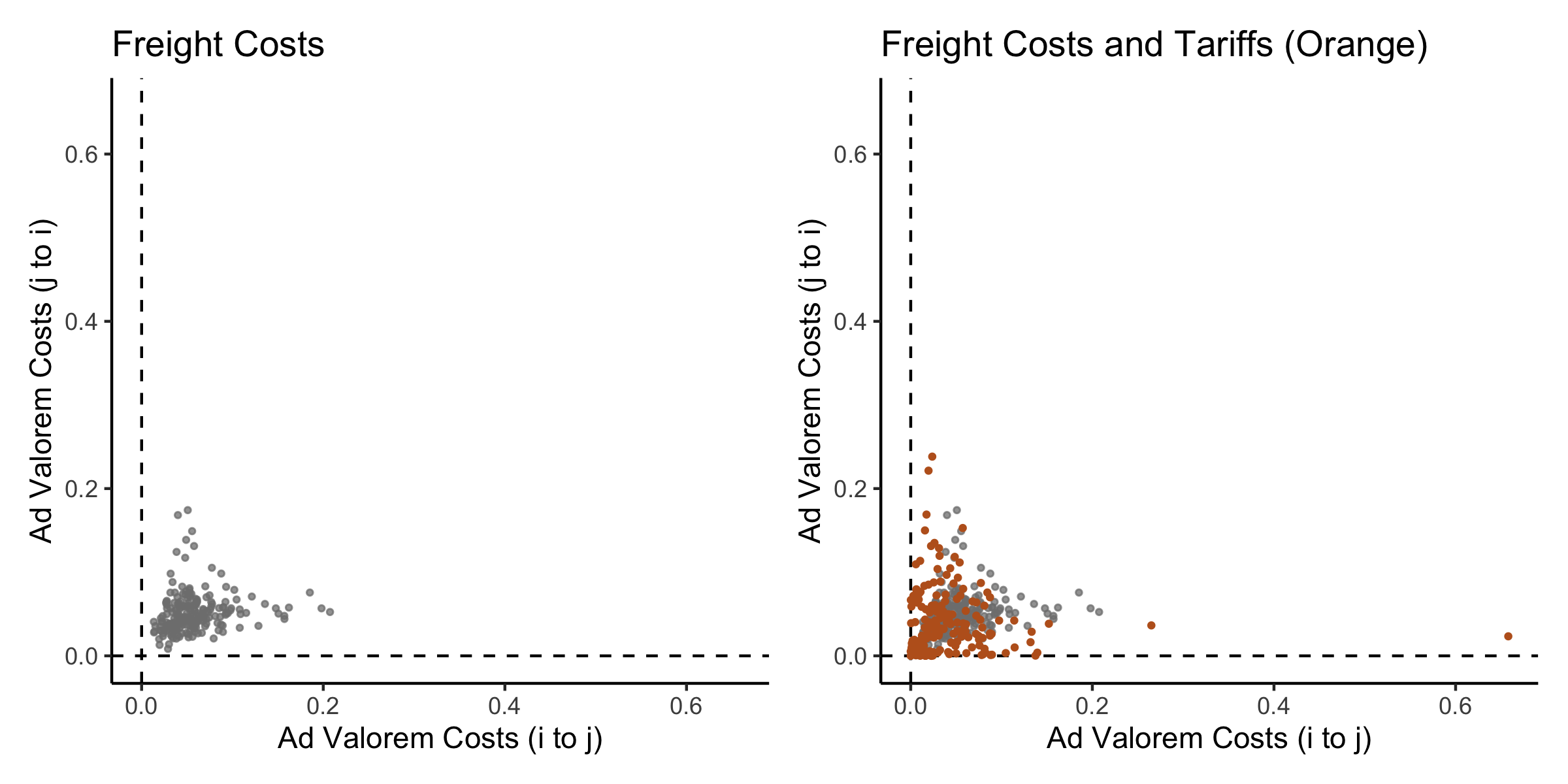
- Data (I): freight costs for shipments to United States, Australia, sample of maritime trade (OECD)
- Data (II): transportation mode shares for United States, Australia, Japan, European Union, and Brazil
- Estimate function \(\delta_{ij}(\bm{Z}_{ij})\) to predict freight costs out of sample
Data and Measurement
\[ \tau_{ij} = \left( \frac{\lambda_{ij}}{\lambda_{jj}} \right)^{-\frac{1}{\theta}} \frac{P_i}{P_j} \frac{1}{\delta_{ij}} \]
- \(\frac{\lambda_{ij}}{\lambda_{jj}}\) - relative expenditure shares
- Data: trade flows and national accounts
- \(\frac{P_i}{P_j}\) - relative price levels
- Data: International Comparison Program (World Bank), good prices and exchange rates
- Estimate preference weights, \(\bm{\alpha}\)
- \(\delta_{ij}(\bm{Z}_{ij})\)
- \(\bm{Z}_{ij}\) dyadic geographic covariates
- Data (I): freight costs for shipments to United States, Australia, sample of maritime trade (OECD)
- Data (II): transportation mode shares for United States, Australia, Japan, European Union, and Brazil
- Estimate function \(\delta_{ij}(\bm{Z}_{ij})\) to predict freight costs out of sample
- Year: 2011
Structural Paramters
\[ \bm{\theta} = \left\{ \sigma, \theta, \bm{\nu} \right\} \]
Expenditure Shares \(\frac{\hat{\lambda}_{ij}}{\hat{\lambda}_{jj}}\)
- Free on board (f.o.b.): value of goods pre-shipment
- Cost, insurance, and freight (c.i.f.): value of goods at port of entry
\[ \lambda_{ij} = \tau_{ij} \lambda_{ij}^{\text{cif}} = \tau_{ij} \delta_{ij} \lambda_{ij}^{\text{fob}} \]
\[ \lambda_{jj}(\bm{\tau}) = \left( 1 - \sum_{k \neq j} \tau_{jk} \lambda_{jk}^{\text{cif}} \right) \]
Expenditure Shares \(\frac{\hat{\lambda}_{ij}}{\hat{\lambda}_{jj}}\)
- Free on board (f.o.b.): value of goods pre-shipment
- Cost, insurance, and freight (c.i.f.): value of goods at port of entry
\[ \lambda_{ij} = \tau_{ij} \lambda_{ij}^{\text{cif}} = \tau_{ij} \delta_{ij} \lambda_{ij}^{\text{fob}} \]
\[ \lambda_{jj}(\bm{\tau}) = \left( 1 - \sum_{k \neq j} \tau_{jk} \lambda_{jk}^{\text{cif}} \right) \]
\[ \color{bcOrange} \lambda_{jk}^{\text{cif}} \color{black} = \frac{X_{jk}^{\text{cif}}}{E_j} \]
- \(X_{jk}^{\text{cif}} = \delta_{ij}(\bm{Z}_{ij}) X_{ij}^{\text{fob}}\)
- \(X_{ij}^{\text{fob}}\) - COMTRADE
- \(E_j = \text{GC}_j - (1 - \nu_j) \text{GDP}_j\) - national accounts (OECD and WIOD)
- \(\nu_j\) - share of income spent on tradables (ICP)
Modified Estimating Equation
\[ \tau_{ij} = \left( \frac{\lambda_{ij}^{\text{cif}}}{ \color{bcOrange} \lambda_{jj}(\bm{\tau}_j) \color{black} } \right)^{-\frac{1}{\theta + 1}} \left( \frac{\hat{P}_i}{\hat{P}_j} \right)^{\frac{\theta}{\theta+1}} \left( \frac{1}{\delta_{ij}(\bm{Z}_{ij})} \right)^{\frac{\theta}{\theta+1}} \]
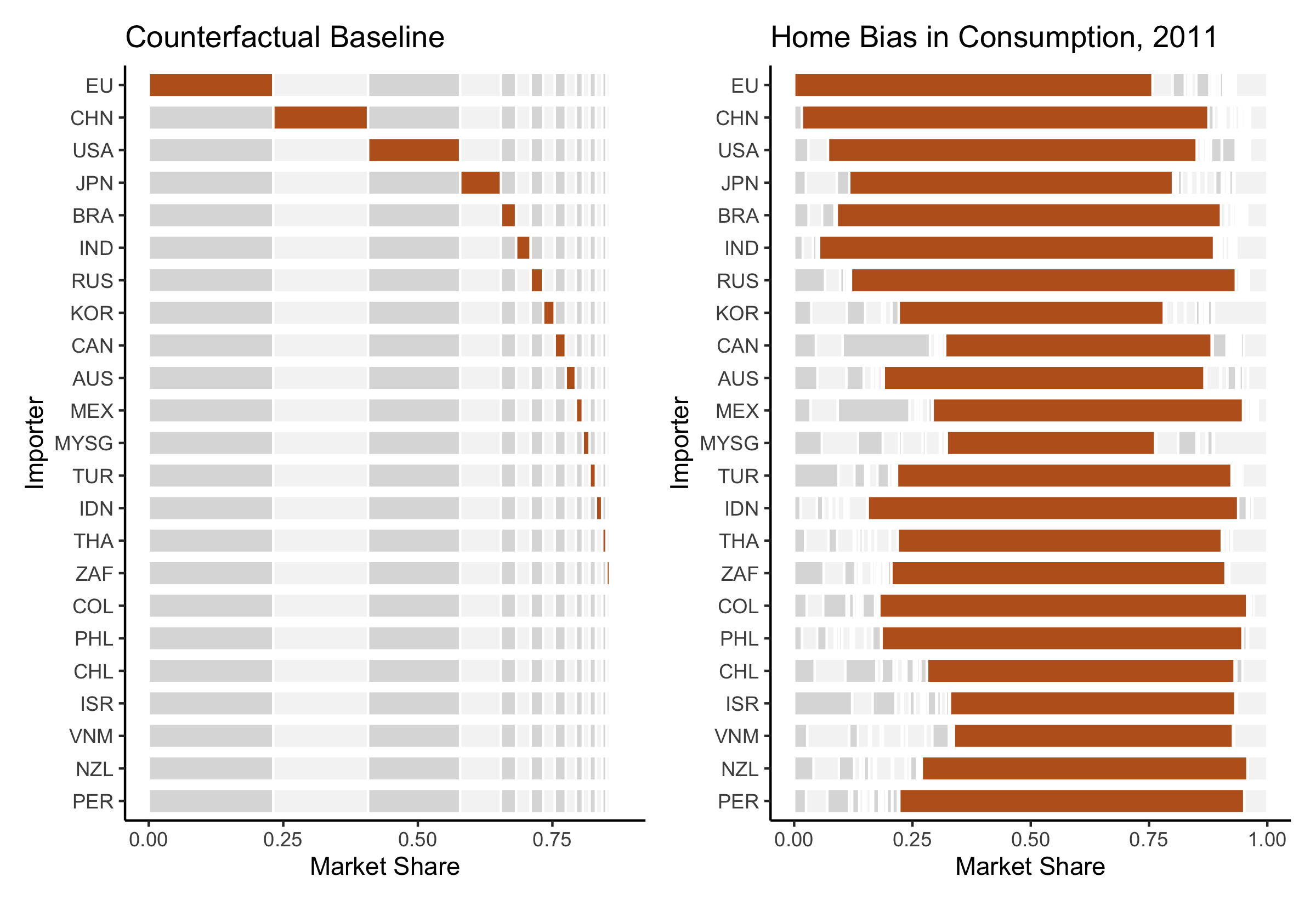
Preliminary Evidence of Significant Barriers
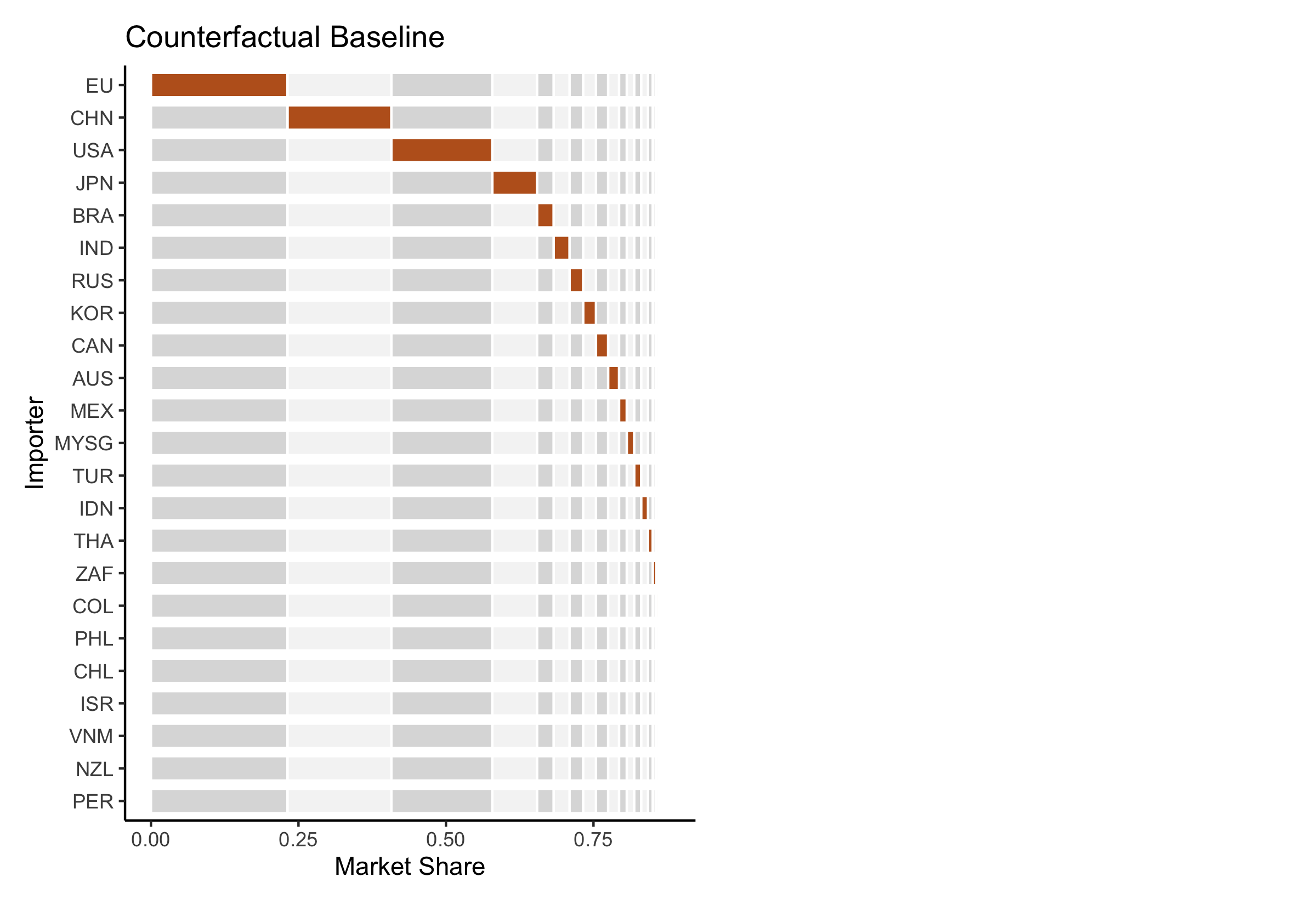
Preliminary Evidence of Significant Barriers
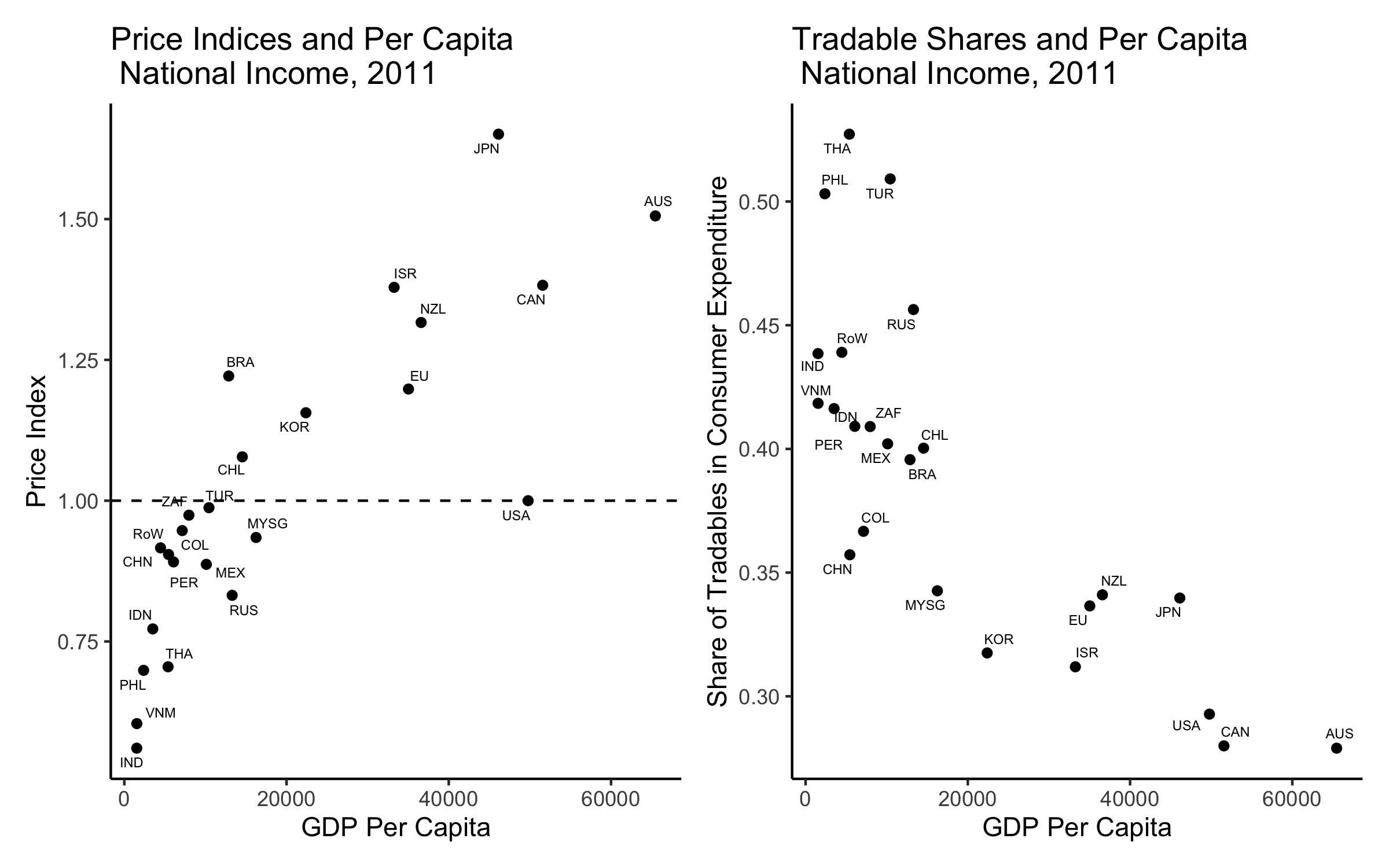
Price Levels \(\frac{\hat{P}_i}{\hat{P}_j}\)
Empirical Price Index
\[ \hat{P}_i(\bm{w}) = \left( \int_{\omega \in [0,1]} \color{bcOrange} \hat{\alpha}_{h(\omega)} \color{black} p_i^\star(\omega)^{1 - \sigma} d \omega \right)^{\frac{1}{1 - \sigma}} \]
Good Categories
\[ h : \Omega \rightarrow \mathcal{K} \]
Assumption: \(p_i(\omega) = p_i(\omega^\prime) = p_{ik}\) for all \(\omega, \omega^\prime \in \Omega_k\)
- \(p_{ik}\) - price in country \(i\) of good ICP basic heading \(k\) (e.g. Rice)
Price Levels \(\frac{\hat{P}_i}{\hat{P}_j}\)
Demand
\[ x_{ik} = \int_{\omega \in \Omega_k} \alpha_k p_{ik}^{1 - \sigma} E_i^q P_i^{\sigma - 1} d \omega \]
Normalization
- \(\alpha_{0} = 1\)
\[ \frac{\lambda_{ik}}{\lambda_{i0}} = \alpha_k \left( \frac{p_{ik}}{p_{i0}} \right)^{1 - \sigma} \]
- \(\frac{\lambda_{ik}}{\lambda_{i0}}\) - basic heading expenditures (ICP)
Estimation
\[ \ln \Delta \lambda_{ik} = \ln \alpha_k + (1 - \sigma) \ln \Delta p_{ik} + \ln \epsilon_{ik} \]
Price Levels (Estimates)
Freight Costs \(\delta_{ij}(\bm{Z}_{ij})\)
- Products \(m \in \left\{ 1, ..., M \right\}\)
- Transportation modes \(o \in \left\{ 1, ..., O \right\}\)
- \(\zeta_{ij}^{m o}\) share of product \(m\) transported by mode \(o\)
- United States, Australia, Japan, European Union, and Brazil
- \(\delta_{ij}^{m o}\)
- United States, Australia, sample of maritime shipments (OECD)
Mode and Cost Functions
\[ g: \left\{ \boldsymbol{Z}_{ij}, d^m \right\} \rightarrow \delta_{ij}^{m o} \] \[ h: \left\{ \boldsymbol{Z}_{ij}, d^m \right\} \rightarrow \zeta_{ij}^{m o} \]
Aggregate Freight Costs
\[ \hat{\delta}_{ij} \left( \boldsymbol{Z}_{ij}, \boldsymbol{d}_{ij} \right) = \frac{1}{X_{ij}} \sum_{m = 1}^M x_{ij}^m \sum_{o=1}^O g \left( \boldsymbol{Z}_{ij}, d^m \right) h \left( \boldsymbol{Z}_{ij}, d^m \right) \]
Freight Costs (Cross Validation)
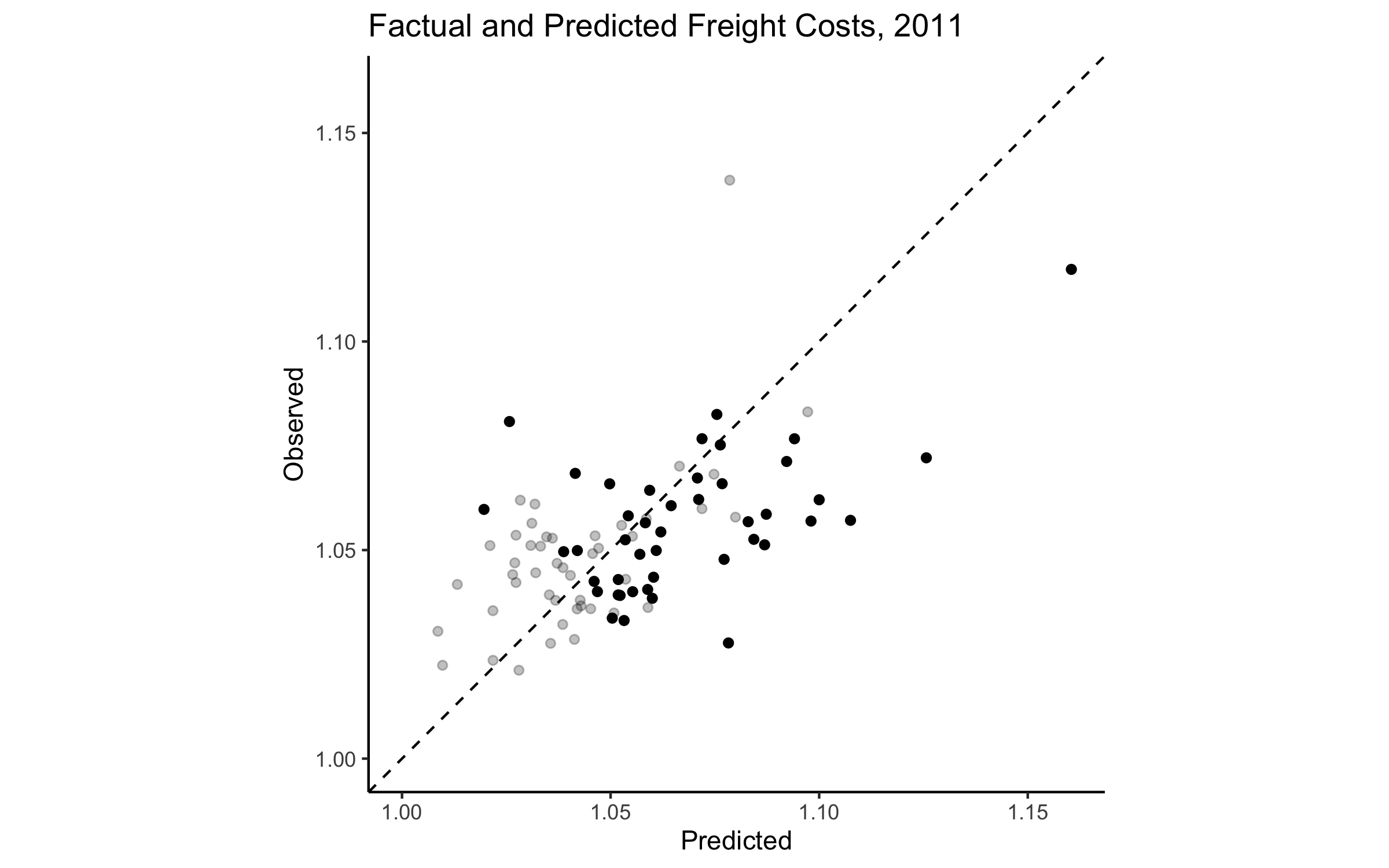
Parameter Calibration
\[ \bm{\theta} = \left\{ \sigma, \theta, \bm{\nu} \right\} \]
- Trade elasticity: \(\sigma - 1 = \theta =\) 6
- Simonovska and Waugh (2014), Head and Mayer (2014)
- \(\bm{\nu}\) - tradable expenditure share (ICP)
Results
Results
\[ \bm{\tau}_{N \times N} = \begin{pmatrix} 1 & \cdots & \tau_{1n} \\ \vdots & \ddots & \vdots \\ \tau_{n1} & \cdots & 1 \end{pmatrix} \]
\[ \tau_{ij} = \left( \frac{\lambda_{ij}^{\text{cif}}}{ \lambda_{jj}(\bm{\tau}_j) } \right)^{-\frac{1}{\theta + 1}} \left( \frac{\hat{P}_i}{\hat{P}_j} \right)^{\frac{\theta}{\theta+1}} \left( \frac{1}{\delta_{ij}(\bm{Z}_{ij})} \right)^{\frac{\theta}{\theta+1}} \]
Results
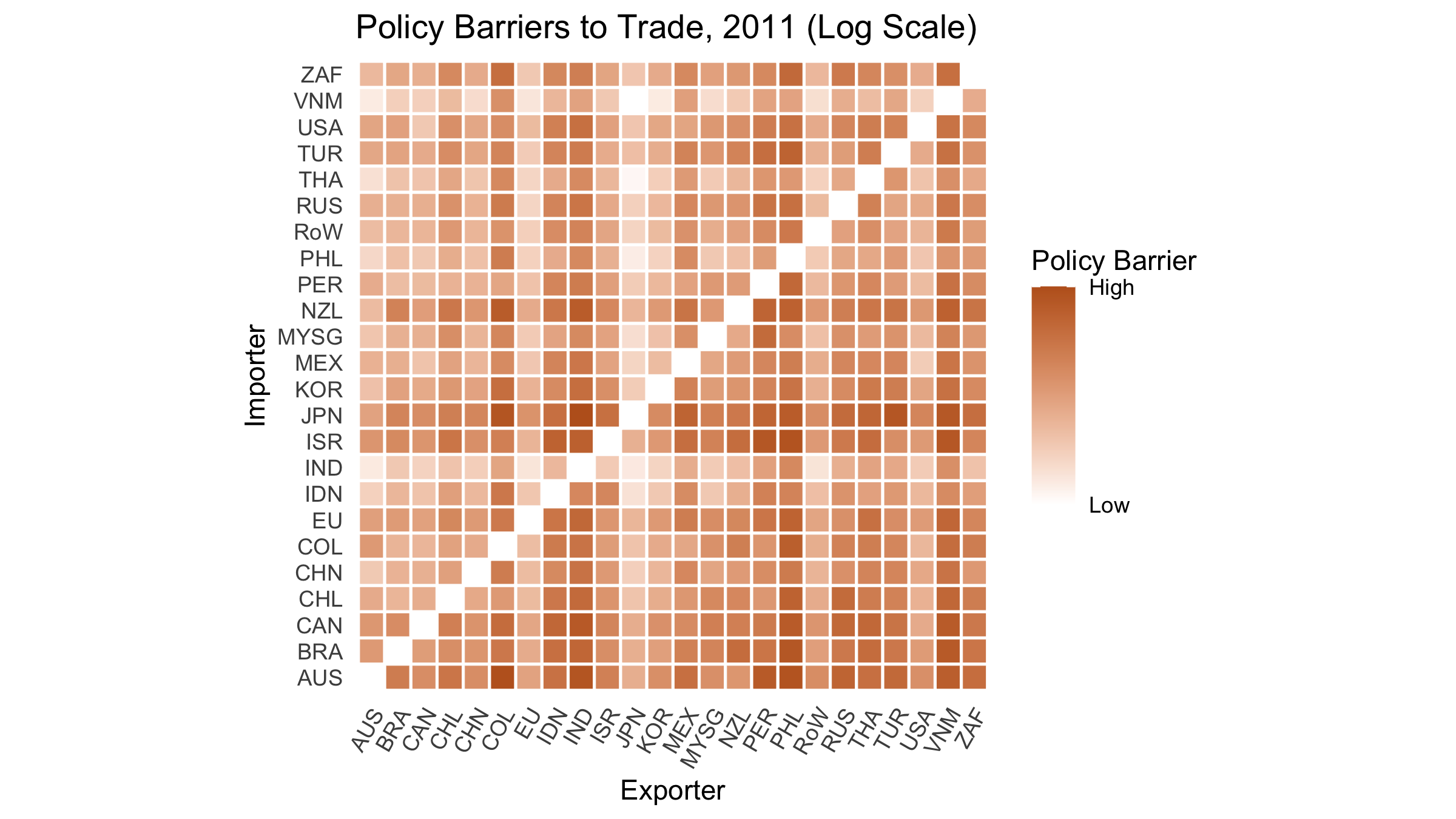
Results
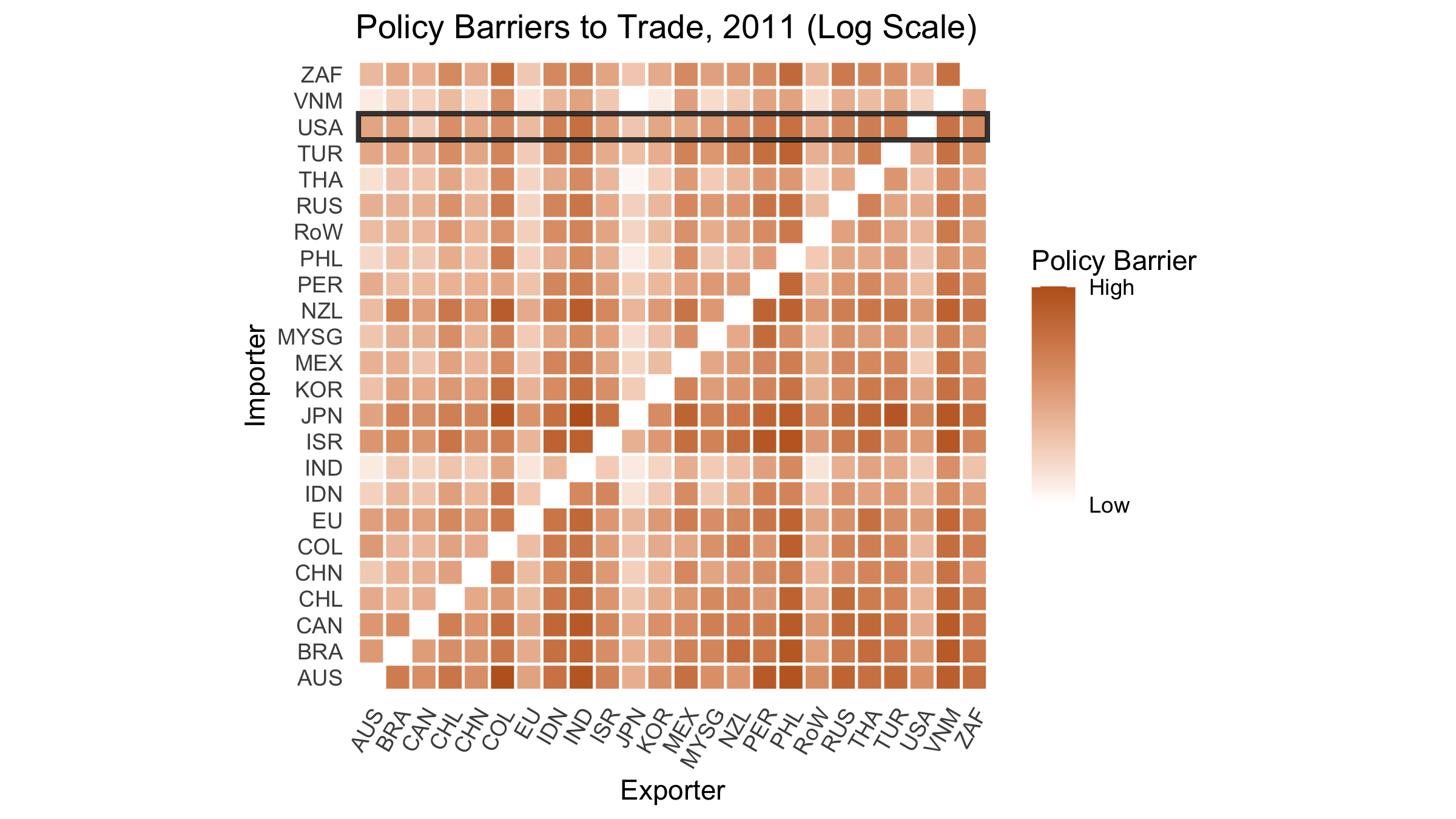
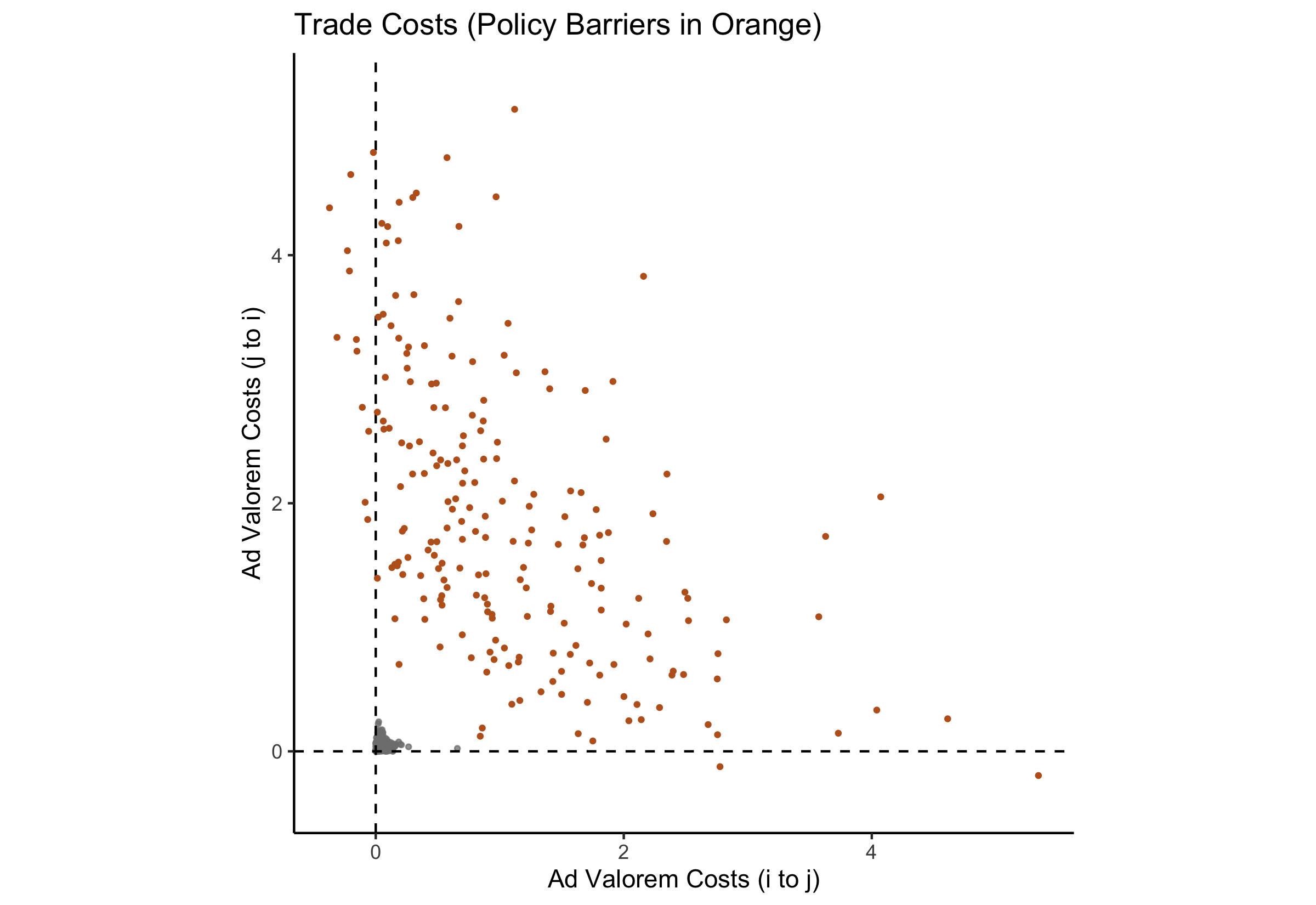
- U.S. favored partners: Canada (19% ad valorem), Japan (21%), EU (40%)
- U.S. disfavored partners: Peru (211%) and Vietnam (260%)
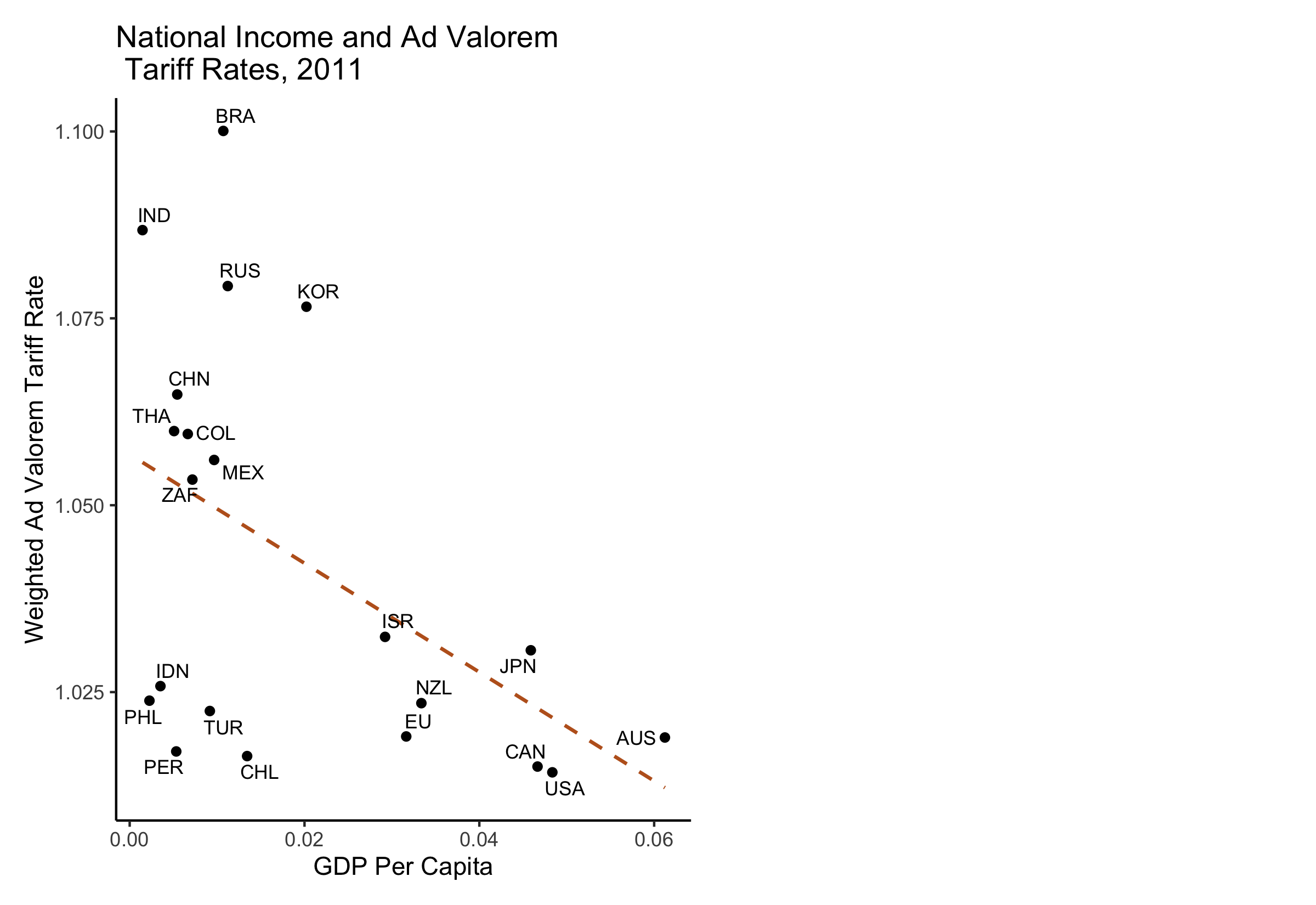
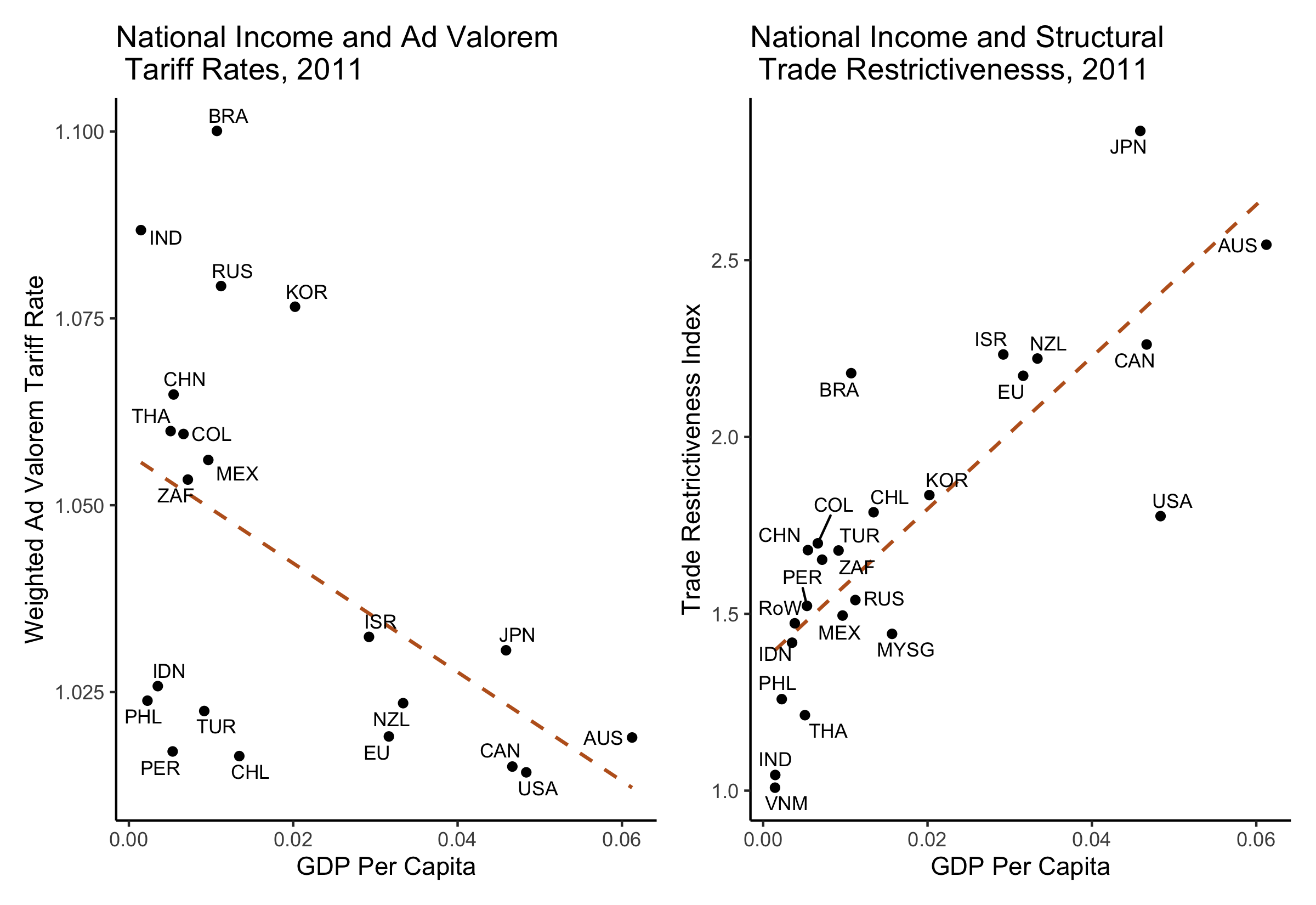
Results (Free?)
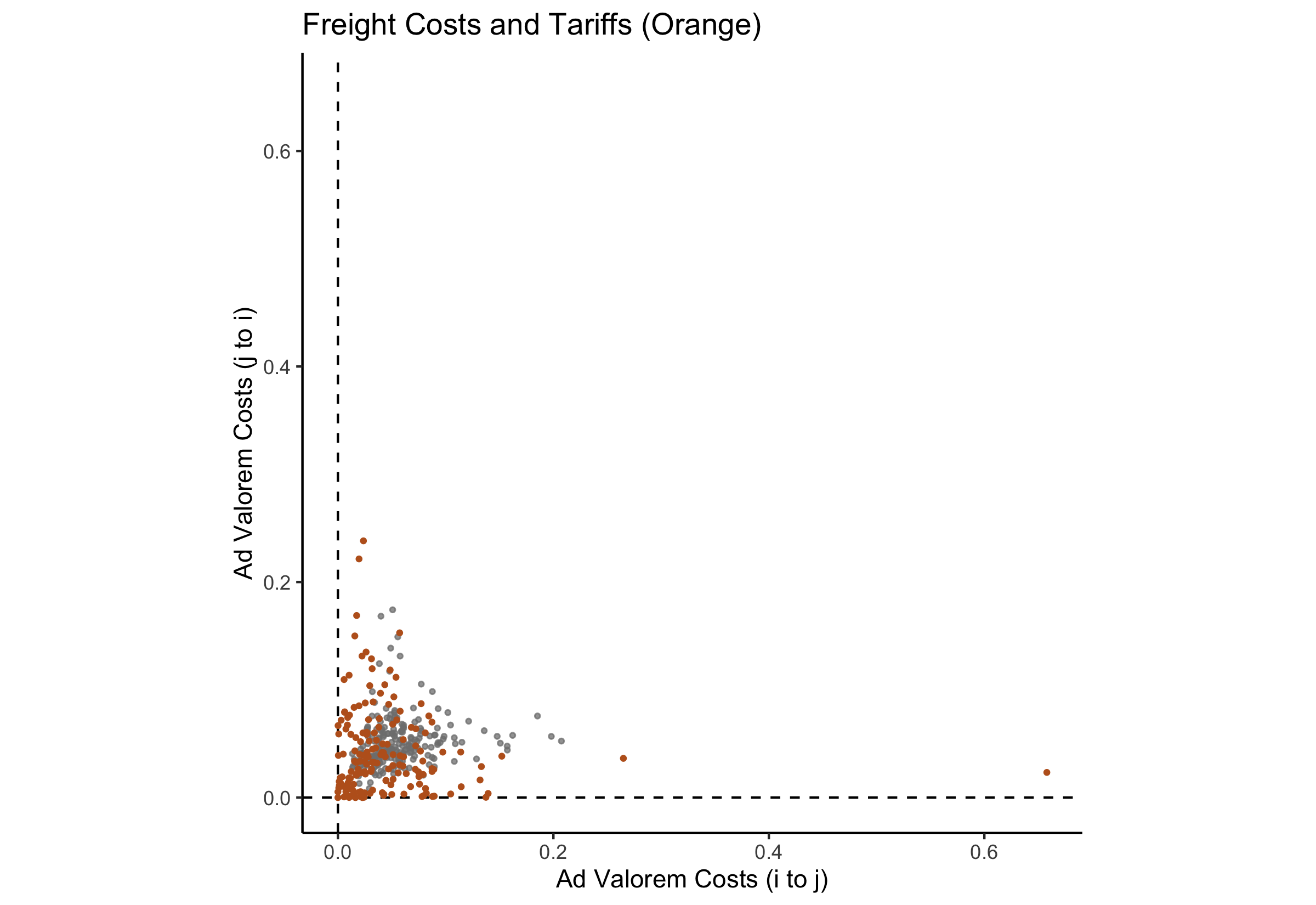
Results (Free?)
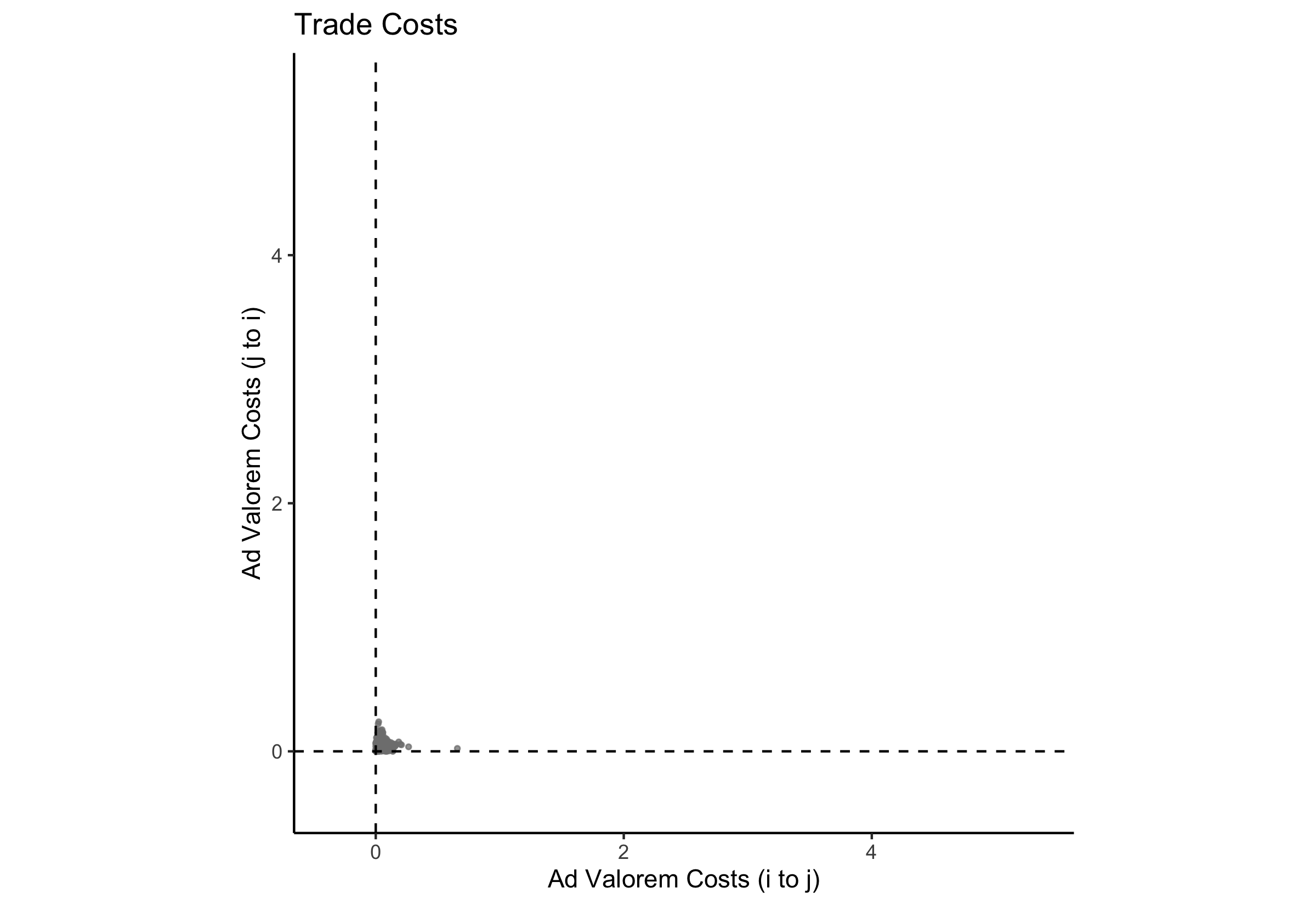
Results (Free?)
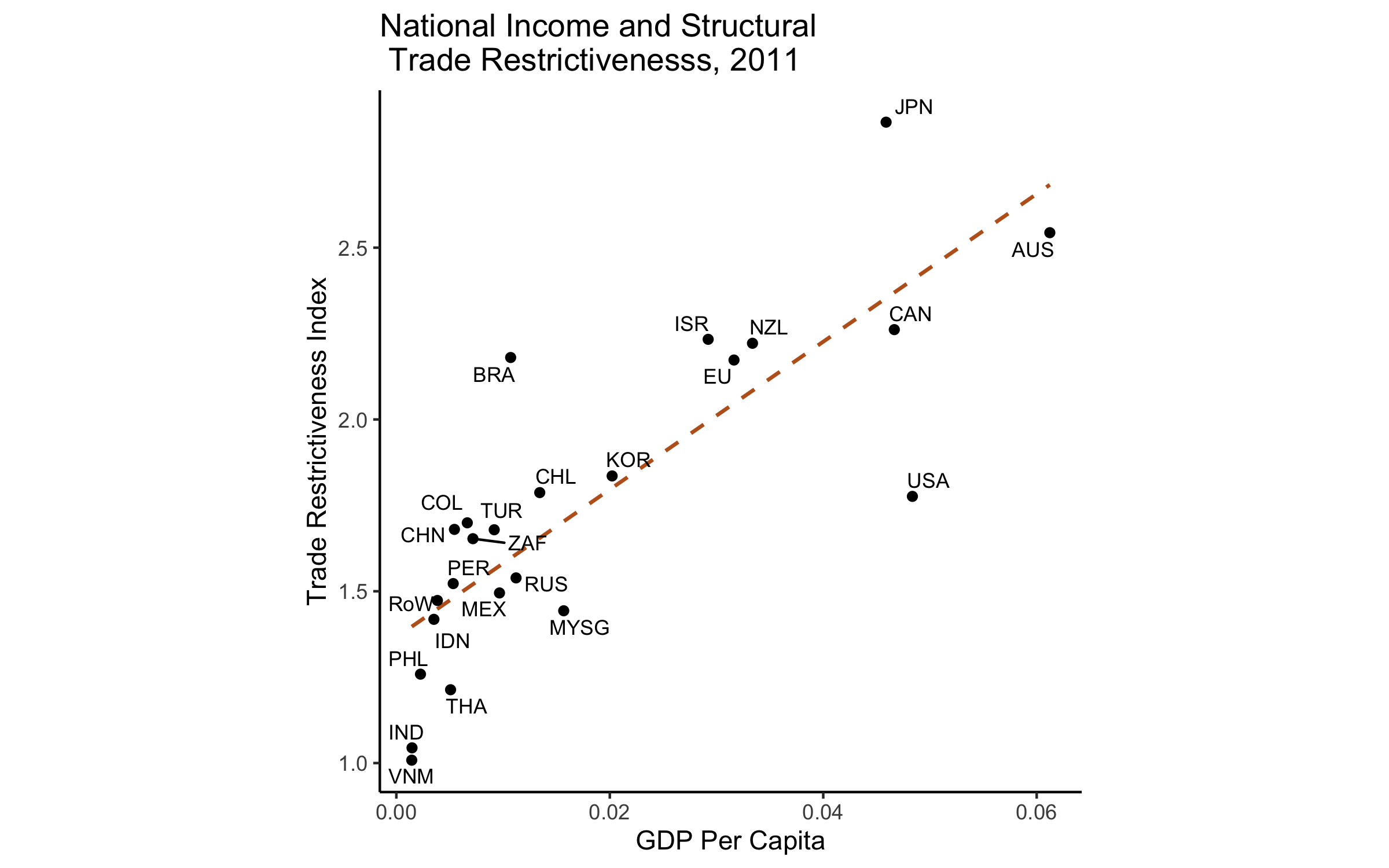
Trade Restrictiveness and Market Access
Trade Restrictiveness Index
\[ \text{TRI}_i = \frac{1}{\sum_{j \neq i} E_j} \sum_{j \neq i} \tau_{ij} E_j \]
Market Access Index
\[ \text{MAI}_j = \frac{1}{\sum_{i \neq j} E_i} \sum_{i \neq j} \tau_{ij} E_i \]
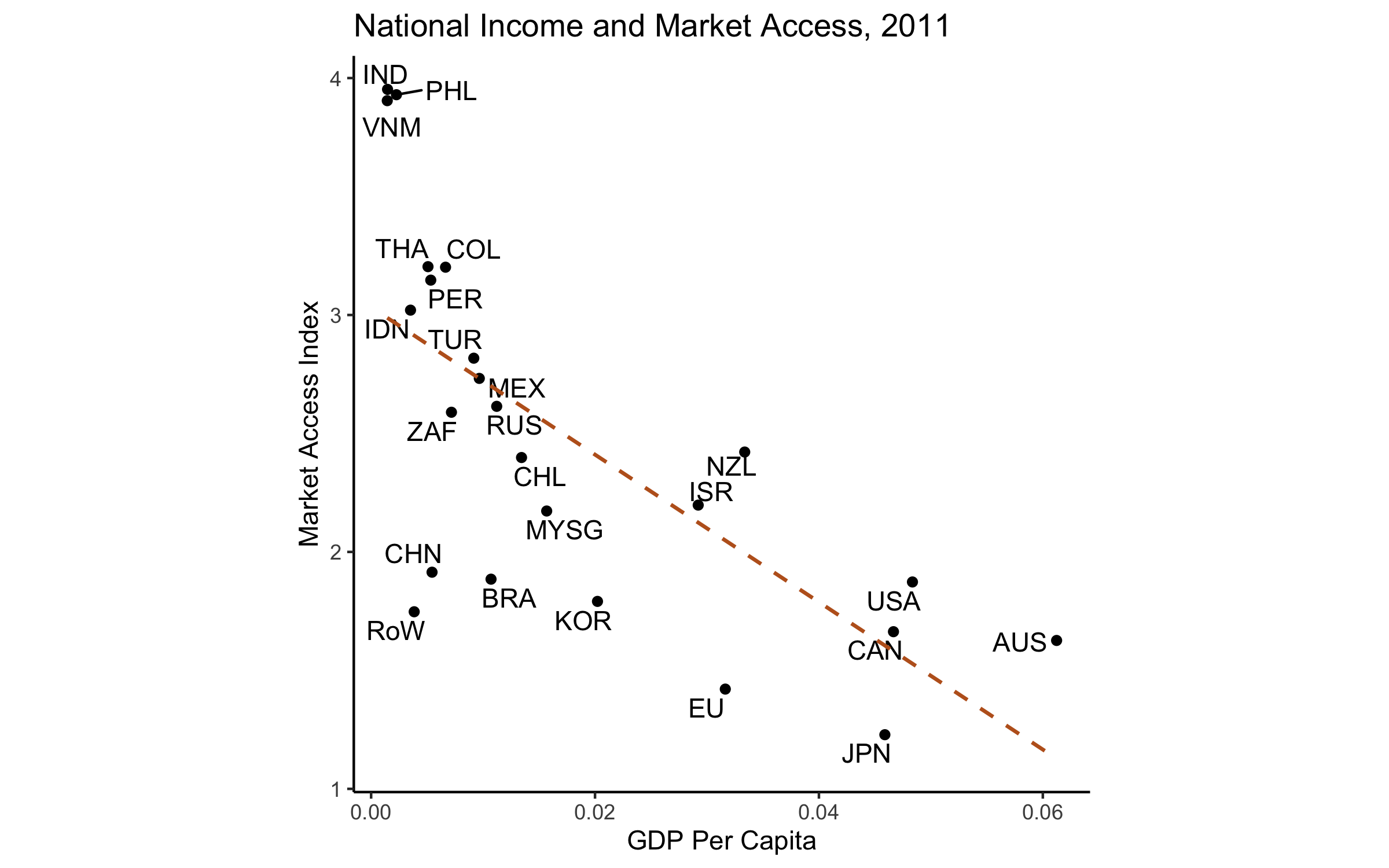
Results (Fair?)
Results (Fair?)
Robustness
Robustness (Correlates)
| DV: Structural Policy Barrier | |
| Tariffs | 1.194** |
| (0.570) | |
| PTAs | -0.316*** |
| (0.063) | |
| Core NTM | 0.097 |
| (0.163) | |
| Health/Safety NTM | 0.171 |
| (0.152) | |
| Other NTM | -0.082 |
| (0.205) | |
| Importer Fixed Effects | Yes |
| Exporter Fixed Effects | Yes |
| N | 361 |
| R2 | 0.876 |
| Notes: | ***Significant at the 1 percent level. |
| **Significant at the 5 percent level. | |
| *Significant at the 10 percent level. | |
Robustness (Intra-European Barriers)
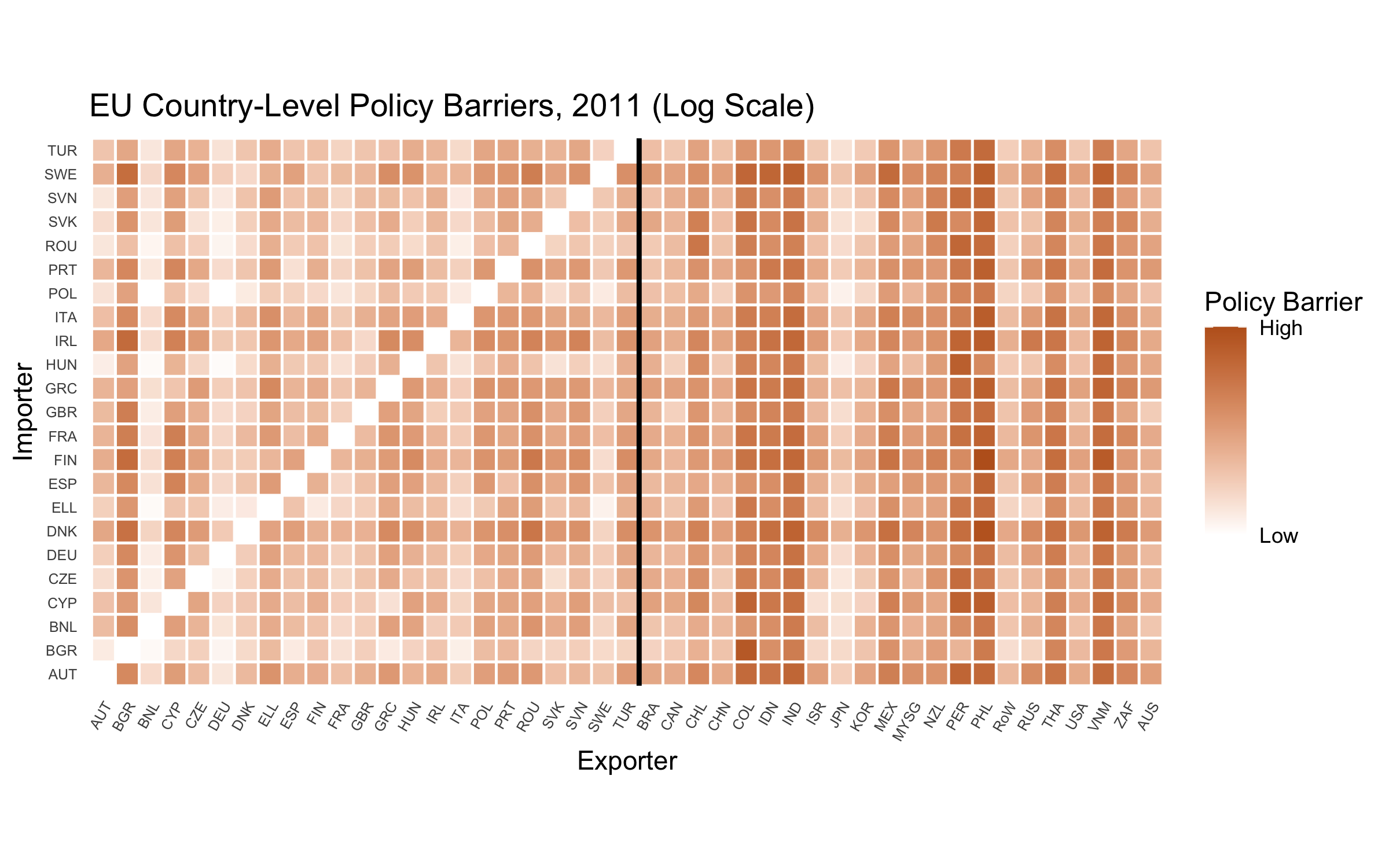
Implications
Implications (Economic Blocs)
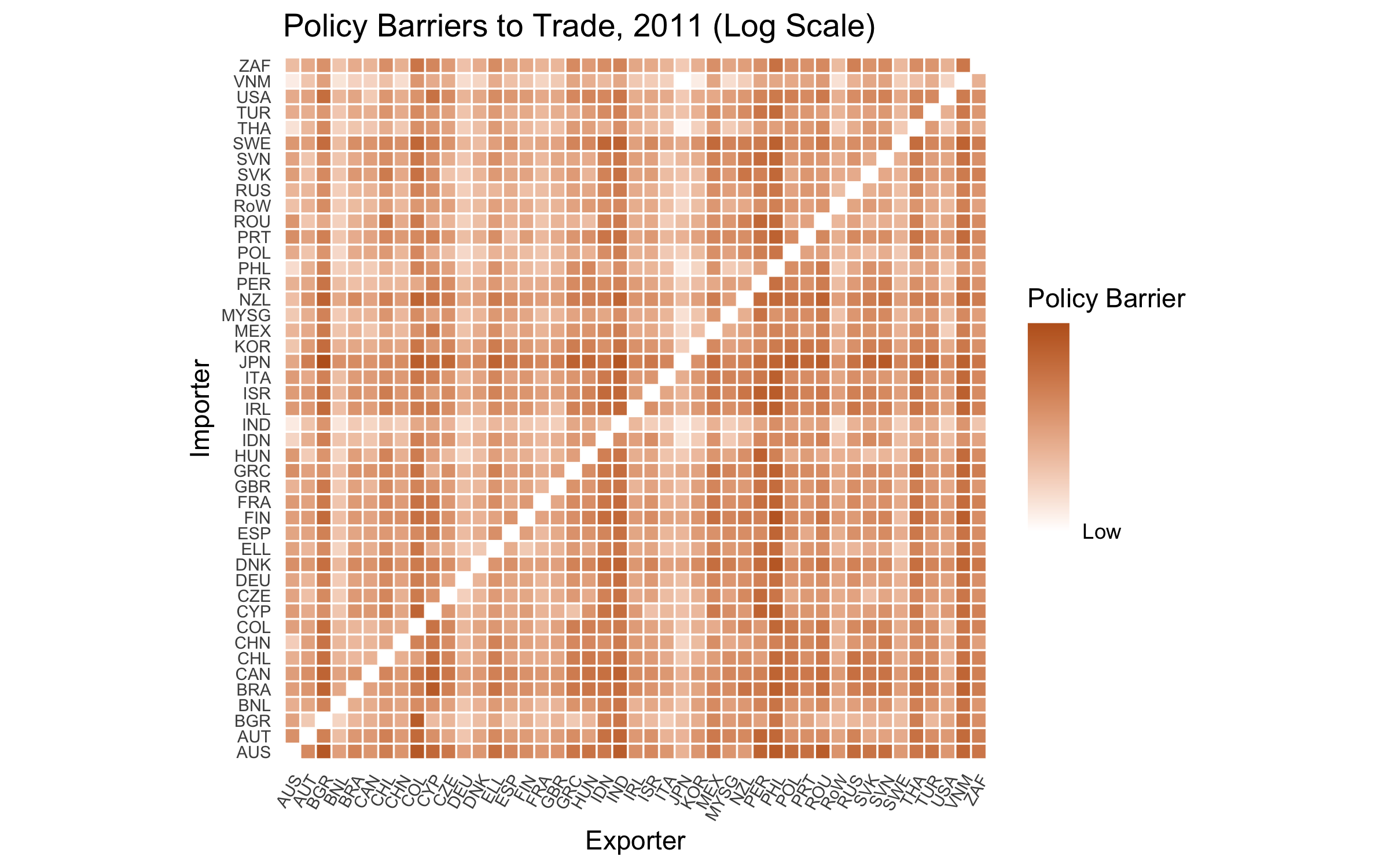
Implications (Economic Blocs)
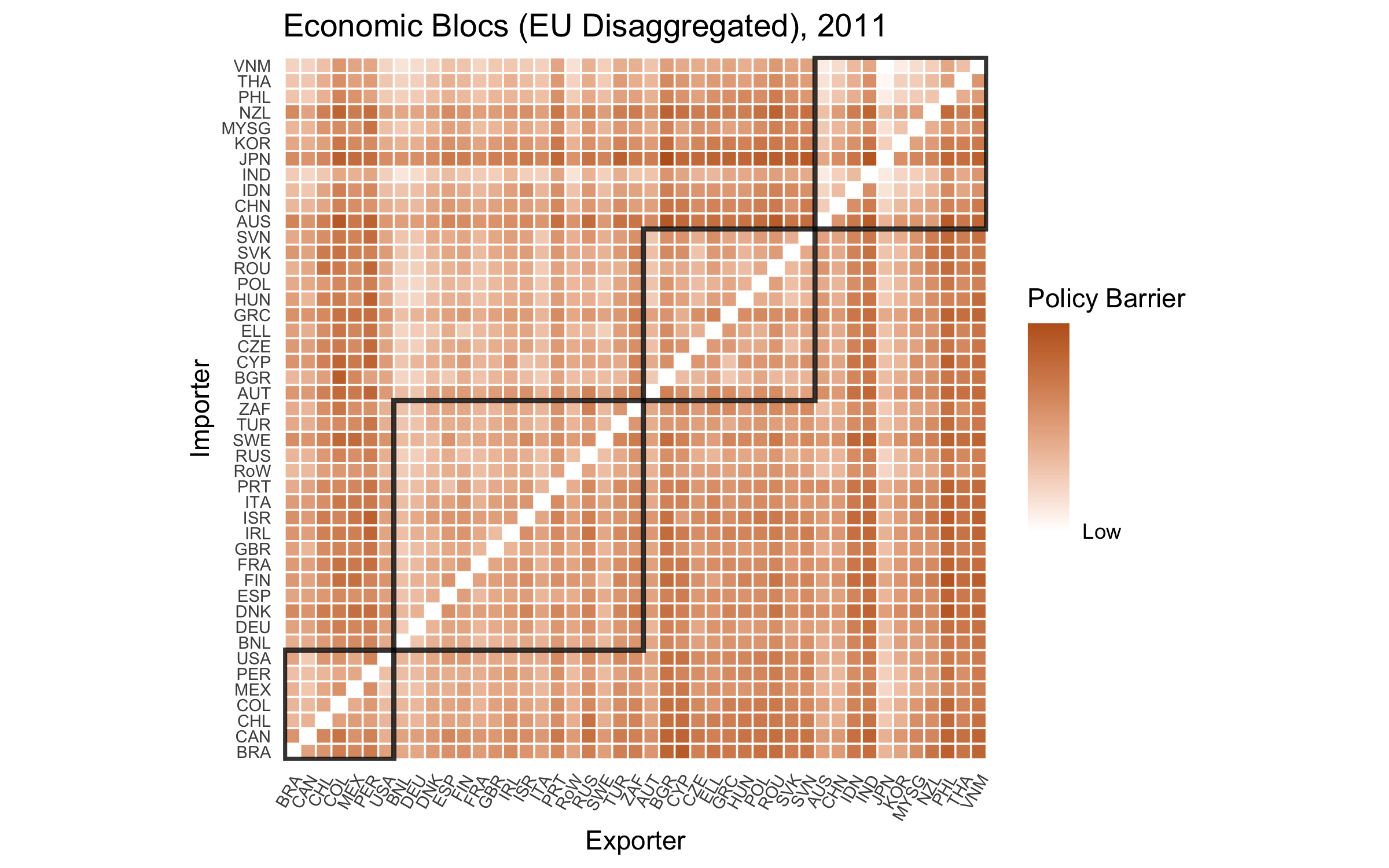
Implications (Democracy and Trade Policy)
- Democracy positively associated with trade restrictiveness
| DV: TRI | |
| gdp (std) | 0.068 |
| (0.068) | |
| polity2 (std) | 0.119* |
| (0.067) | |
| N | 39 |
| R2 | 0.087 |
| Notes: | ***Significant at the 1 percent level. |
| **Significant at the 5 percent level. | |
| *Significant at the 10 percent level. | |
Conclusion
Conclusion
Nondiscrimination in the Trade Regime
- Almost all countries in sample are WTO members, but substantial effective discrimination persists
- Contra Bagwell and Staiger (1999), Maggi (1999), Bown (2004)
- PTAs negatively associated with barriers
- Importance of behind-the-border barriers, regulatory harmonization, “deep integration” (Baccini 2019)
Democracy, Development, and Trade Policy
- Democracies less liberal than autocracies
- Contra Milner and Kubota (2005), Eichengreen and Leblang (2008), Gawande, Krishna, and Olarreaga (2009), Gawande, Krishna, and Olarreaga (2015), Barari, Kim, and Wong (n.d.) (tariffs)
- Tariffs as “second-best” solution to revenue-raising problem facing low-capacity governments
- Acemoglu (2005), Rodrik (2008), and Queralt (2015)
Thank You
Table of Contents
Sections
Appendix
Fréchet Distribution
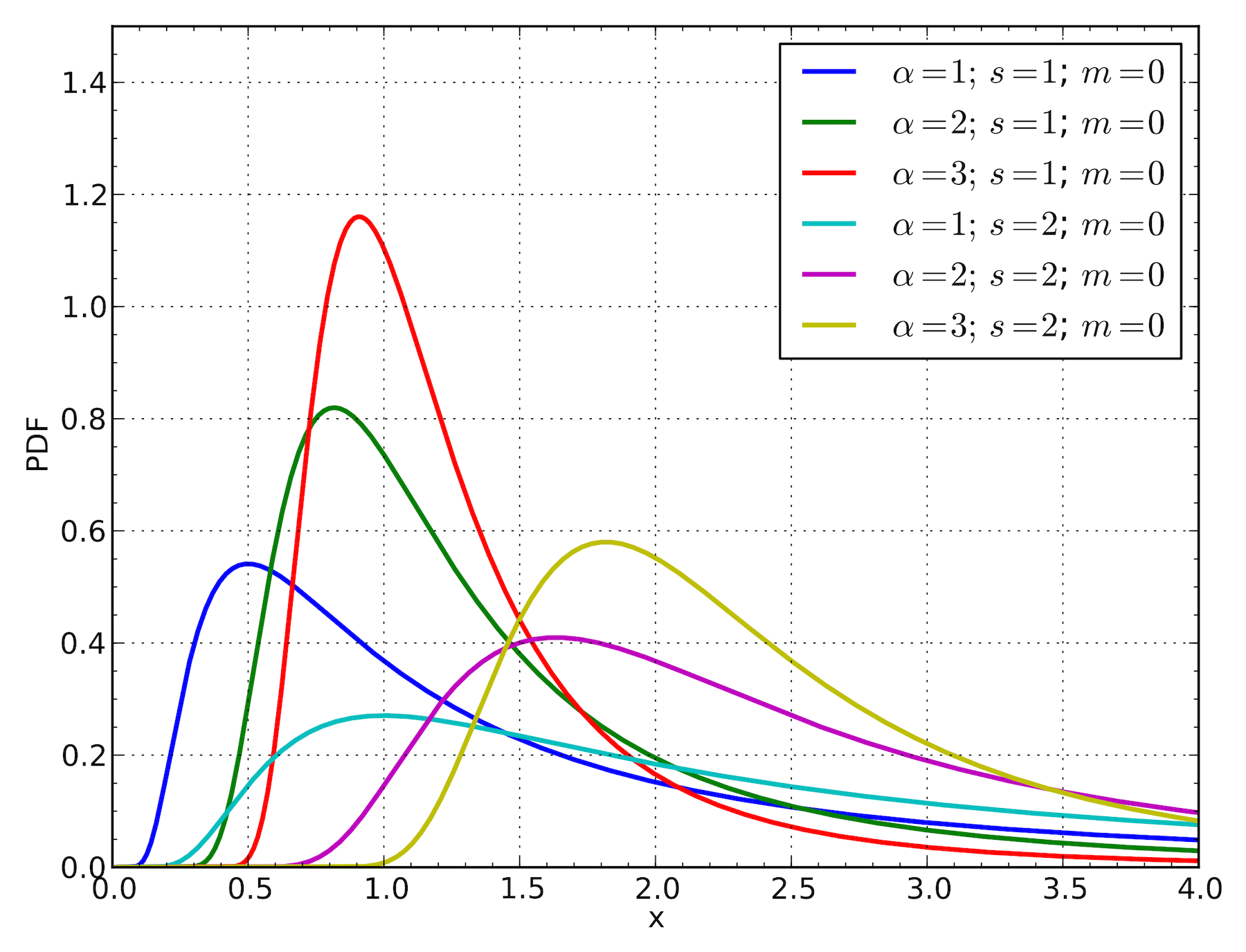
Acemoglu, Daron. 2005. “Politics and economics in weak and strong states.” Journal of Monetary Economics 52 (7): 1199–1226.
Alvarez, Fernando, and Robert E Lucas. 2007. “General equilibrium analysis of the Eaton–Kortum model of international trade.” Journal of Monetary Economics 54: 1726–68.
Anderson, James E, and Eric Van Wincoop. 2003. “Gravity with Gravitas: A Solution to the Border Puzzle.” The American Economic Review 93 (1): 170–92.
Baccini, Leonardo. 2019. “The Economics and Politics of Preferential Trade Agreements.” Annual Review of Political Science 22.
Bagwell, Kyle, and Robert W. Staiger. 1999. “An economic theory of GATT.” American Economic Review 89 (1): 215–48.
Baldwin, Richard. 2016. “The World Trade Organization and the Future of Multilateralism.” Journal of Economic Perspectives 30: 95–116.
Barari, Soubhik, In Song Kim, and Weihuang Wong. n.d. “Trade Liberalization and Regime Type: Evidence from a New Tariff-line Dataset.” http://web.mit.edu/insong/www/pdf/poltrade.pdf.
Bown, Chad P. 2004. “Trade policy under the GATT/WTO: empirical evidence of the equal treatment rule.” Canadian Journal of Economics/Revue Canadienne d‘Economique 37 (3): 678–720.
Chaney, Thomas. 2008. “Distorted Gravity: The Intensive and Extensive Margins of International Trade.” American Economic Review 98 (4): 1707–21.
Costinot, Arnaud, and Andrés Rodríguez-Clare. 2015. “Trade Theory with Numbers: Quantifying the Consequences of Globalization.” Handbook of International Economics 4: 197–261.
Eaton, Jonathan, and Samuel Kortum. 2002. “Technology, geography, and trade.” Econometrica 70 (5): 1741–79.
Eichengreen, Barry, and David Leblang. 2008. “Democracy and Globalization.” Economics & Politics 20 (3): 289–334.
Evenett, Simon J., and Bernard Hoekman. 2004. Government Procurement: Market Access, Transparency, and Multilateral Trade Rules. Policy Research Working Papers. The World Bank.
Gawande, Kishore, and Wendy L. Hansen. 1999. “Retaliation, Bargaining, and the Pursuit of "Free and Fair" Trade.” International Organization 53 (1): 117–59.
Gawande, Kishore, Pravin Krishna, and Marcelo Olarreaga. 2009. “What governments maximize and why: the view from trade.” International Organization 63 (03): 491–532.
———. 2015. “A Political-Economic Account of Global Tariffs.” Economics & Politics 27 (2): 204–33.
Head, Keith, and Thierry Mayer. 2014. “Gravity Equations: Workhorse, Toolkit and Cookbook.” In Handbook of International Economics, edited by Elhanan Helpman, G. Gopinath, and K. Rogoff, 4th ed., 131–96.
Kono, Daniel Yuichi. 2006. “Optimal obfuscation: Democracy and trade policy transparency.” American Political Science Review 100 (03): 369–84.
Kono, Daniel Yuichi, and Stephanie J Rickard. 2014. “Buying National: Democracy, Public Procurement, and International Trade.” International Interactions 40 (5): 657–82.
Lee, Jong-Wha, and Phillip Swagel. 1997. “Trade Barriers and Trade Flows Across Countries and Industries.” The Review of Economics and Statistics 79 (3): 372–82.
Maggi, Giovanni. 1999. “The role of multilateral institutions in international trade cooperation.” American Economic Review, 190–214.
Maggi, Giovanni, Monika Mrázová, and J Peter Neary. 2018. “Choked by Red Tape? The Political Economy of Wasteful Trade Barriers.”
Mansfield, Edward D., and Marc L. Busch. 1995. “The Political Economy of Nontariff Barriers: A Cross-National Analysis.” International Organization 49 (4): 723–49.
Melitz, Marc J. 2003. “The impact of trade on intra-industry reallocations and aggregate industry productivity.” Econometrica 71 (6): 1695–1725.
Milner, Helen V, and Keiko Kubota. 2005. “Why the move to free trade? Democracy and trade policy in the developing countries.” International Organization 59 (01): 107–43.
Queralt, Didac. 2015. “From Mercantilism to Free Trade: A History of Fiscal Capacity Building.” Quarterly Journal of Political Science 10: 221–73.
Rickard, Stephanie J. 2012. “A Non-Tariff Protectionist Bias in Majoritarian Politics: Government Subsidies and Electoral Institutions.” International Studies Quarterly 56: 777–85.
Rodrik, Dani. 2008. “Second-Best Institutions.” American Economic Review: Papers & Proceedings 98 (2): 100–104.
Simonovska, Ina, and Michael E Waugh. 2014. “The Elasticity of Trade: Estimates and Evidence.” Journal of International Economics 92 (1): 34–50.
Sposi, Michael. 2015. “Trade barriers and the relative price of tradables.” Journal of International Economics 96 (2): 398–411.
Waugh, Michael E. 2010. “International Trade and Income Differences.” American Economic Review 100: 2093–2124.
Waugh, Michael E, and B Ravikumar. 2016. “Measuring Openness to Trade.” Journal of Economic Dynamics and Control 72: 29–41.