\[ \require{color} \definecolor{bcOrange}{RGB}{189,97,33} \definecolor{bcYellow}{RGB}{189,142,40} \newcommand\iddots{\mathinner{ \kern1mu\raise1pt{.} \kern2mu\raise4pt{.} \kern2mu\raise7pt{\Rule{0pt}{7pt}{0pt}.} \kern1mu }} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\bm}[1]{\boldsymbol{\mathbf{#1}}} \newcommand{\ubar}[1]{\underline{#1}} \]

Gunshots and Turf Wars:

Inferring Gang Territories from Administrative Data

18 September 2020

Brendan Cooley | Noam Reich

Ph.D. Candidates

Princeton University

bcooley (at) princeton.edu | noamg (at) princeton.edu

These slides available at brendancooley.com/gangs

Introduction

Gunshots and Turf Wars

Gunshots

“In 2006 nearly 50 percent of the homicides and a large percentage of other violent crimes and property crimes committed in Chicago were attributed to street gangs that are involved in drug trafficking”

  • National Drug Intelligence Center (2007)
  • Inter- and intra-gang conflict in gang ethnographies
    • Sanchez-Jankowski (1991), Decker (1996), Levitt and Venkatesh (2000), Papachristos (2009)
  • Not unique to Chicago
    • Howell and Griffiths (2018)

Turf Wars

“Gang violence is often sparked by competitive relations over turf. A gang’s turf has economic and symbolic value: the gang regulates who sells what on its street corners, and gang members take pride in controlling the blocks where they grew up. Encroaching on another gang’s turf can trigger violence and a series of retaliations as gang members avenge fallen comrades.”

  • Vargas (2016), Wounded City
  • Territorial rent-seeking: racketerring, drug-selling monopolies, smuggling
    • Thrasher (1927), Sanchez-Jankowski (1991), Levitt and Venkatesh (2000), Venkatesh and Levitt (2000)
  • Conflict over rent streams and challenges to reputations
    • Brantingham et al. (2012), Papachristos, Hureau, and Braga (2013), Vargas (2016), Bueno De Mesquita (2018)

Measurement Problem

  • Territorial conflict between rival gangs is responsible for much of the violence in American cities
  • Problem: gangs are covert organizations \(\implies\) knowledge of gangs remains anecdotal and spatially circumscribed

First-Order Descriptive Questions

  1. How many gangs operate within a given municipality?
  2. How is territory divided amongst them?

Existing Approaches

  • Police Records: Bruhn (2019) (Chicago), Melnikov, Schmidt-Padilla, and Sviatschi (2019) (San Salvador)
    • Not broadly available or not shared with public
    • Reporting biases and auditability: how are data constructed?
  • Newspapers, NLP, Mixed Methods (Blattman et al. 2019; Sobrino 2019; Signoret 2020)
    • Require deep subject matter expertise, difficult to generalize beyond target locale

Approach

Observables: Time-stamped, geolocated homicides and nonfatal shootings

  • Widely available in administrative records on crime

Unobservables:

  1. Number of gangs
  2. Territorial partition

Inferential Strategy

  1. Model data-generating process for shootings
    • Non-gang
    • Intra-gang
    • Inter-gang
  1. Derive relationship between spatial covariance in shootings and unobservables
    • Generalization of Trebbi and Weese (2019) to inter-group conflict
    • Akin to stochastic block model (SBM) (Holland, Laskey, and Leinhardt 1983)
  1. Estimate model using observed spatial covariances
    • Spectral clustering (Luxburg 2007; Lei and Rinaldo 2015; Chen and Lei 2018)
  1. Validate results using Chicago Police Department (CPD) gang maps (Bruhn 2019)
    • Match partition function labels to those of CPD

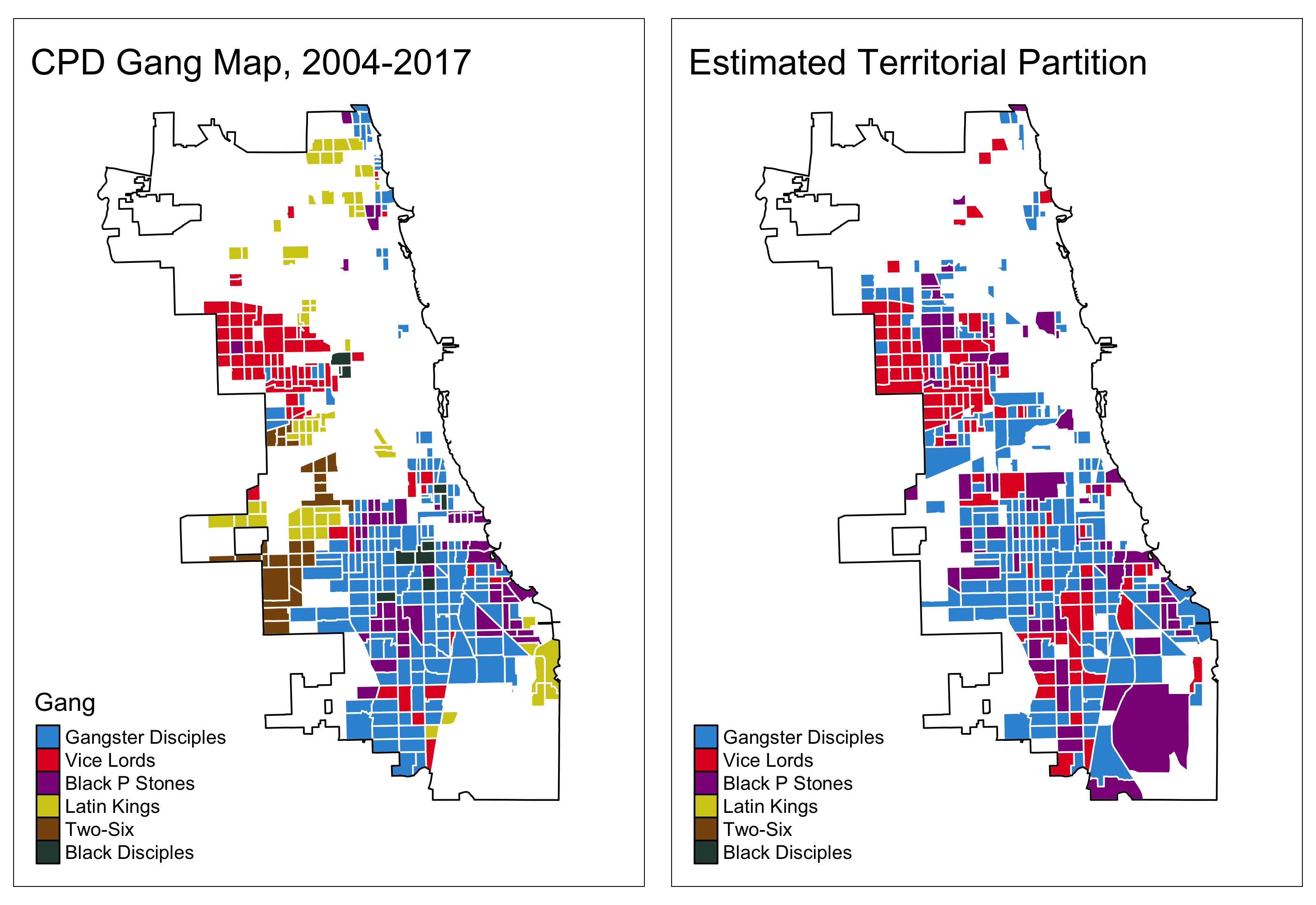
Bottom Line

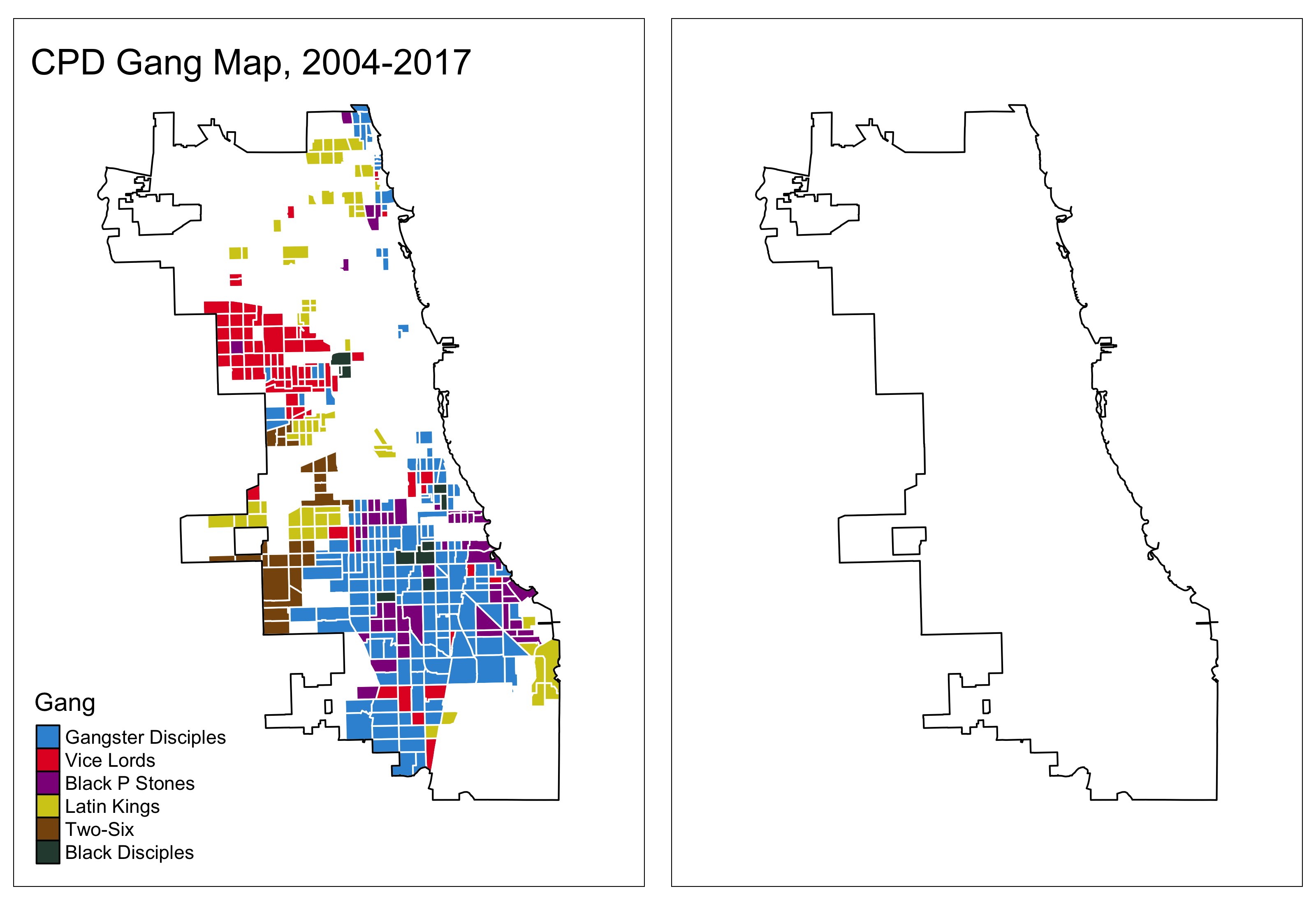
Bottom Line

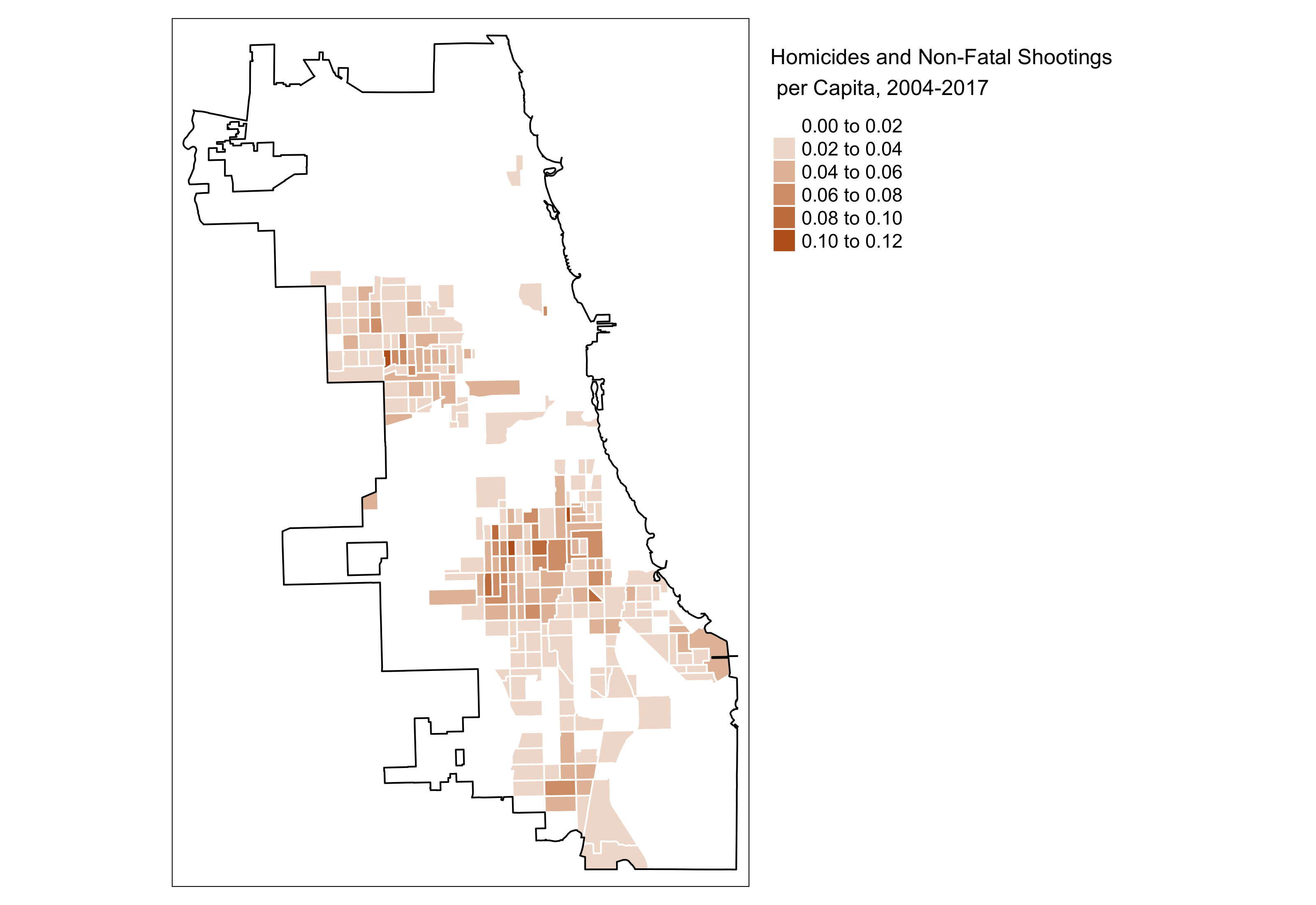
Data

Data

Gunshots (Data): Victim-based crime reports, 2004-2017 (CLEAR)

  • Illinois Uniform Crime Reporting code, latitude, longitude, date-time
  • Extract homicides and nonfatal shootings (aggravated battery with firearm), 32,236 events
  • Project into census tract-months: 861 tracts, ~4,000 residents each

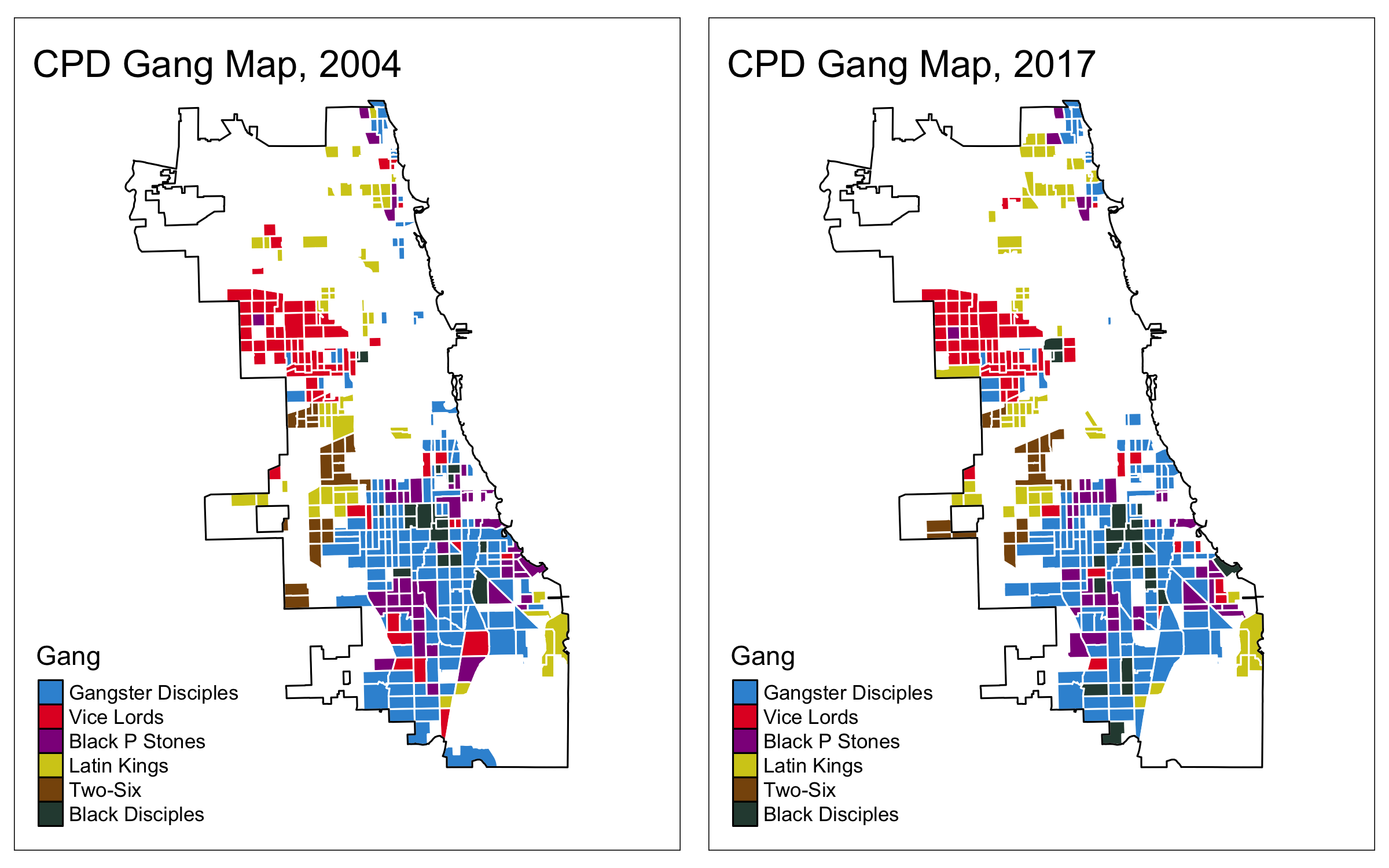
Turf (Validation): CPD internal reports, annual (Bruhn 2019)

  • Report number of gangs and territorial partition, 2004-2017
  • Collapse panel
    • Take average territorial footprint over sample period
  • Preprocessing
    • 55 gangs total, focus on 6 largest by territorial extent for validation
    • These control 77% of all gang turf
  • Assign a tract to a gang if 1) it owns plurality of tract area and 2) it owns at least 10 percent of tract
    • 39 satisfy criteria for inclusion

Territorial Distribution

Ethnicity

Gunshots, Spatial Distribution

Gunshots, Panel Construction

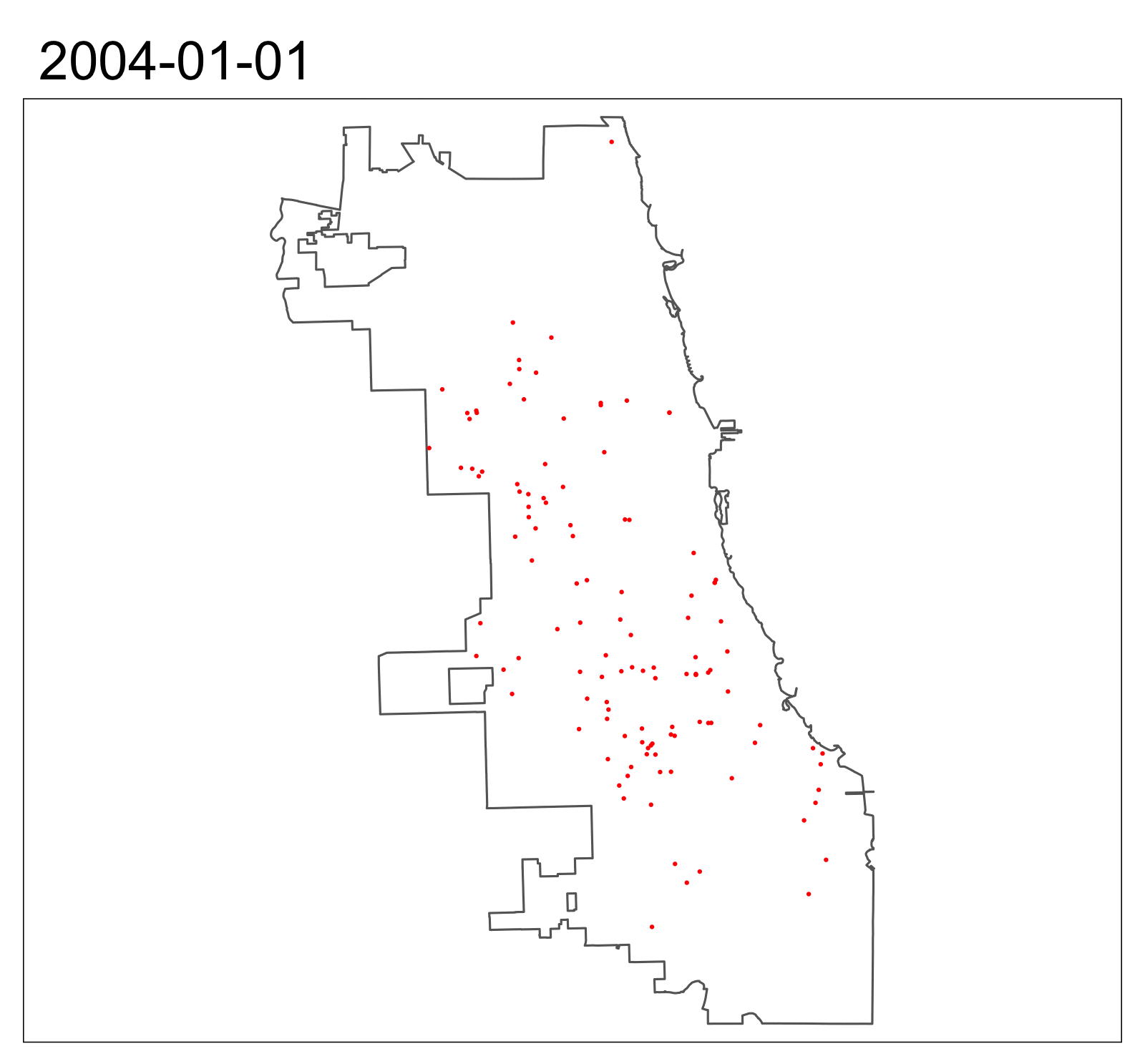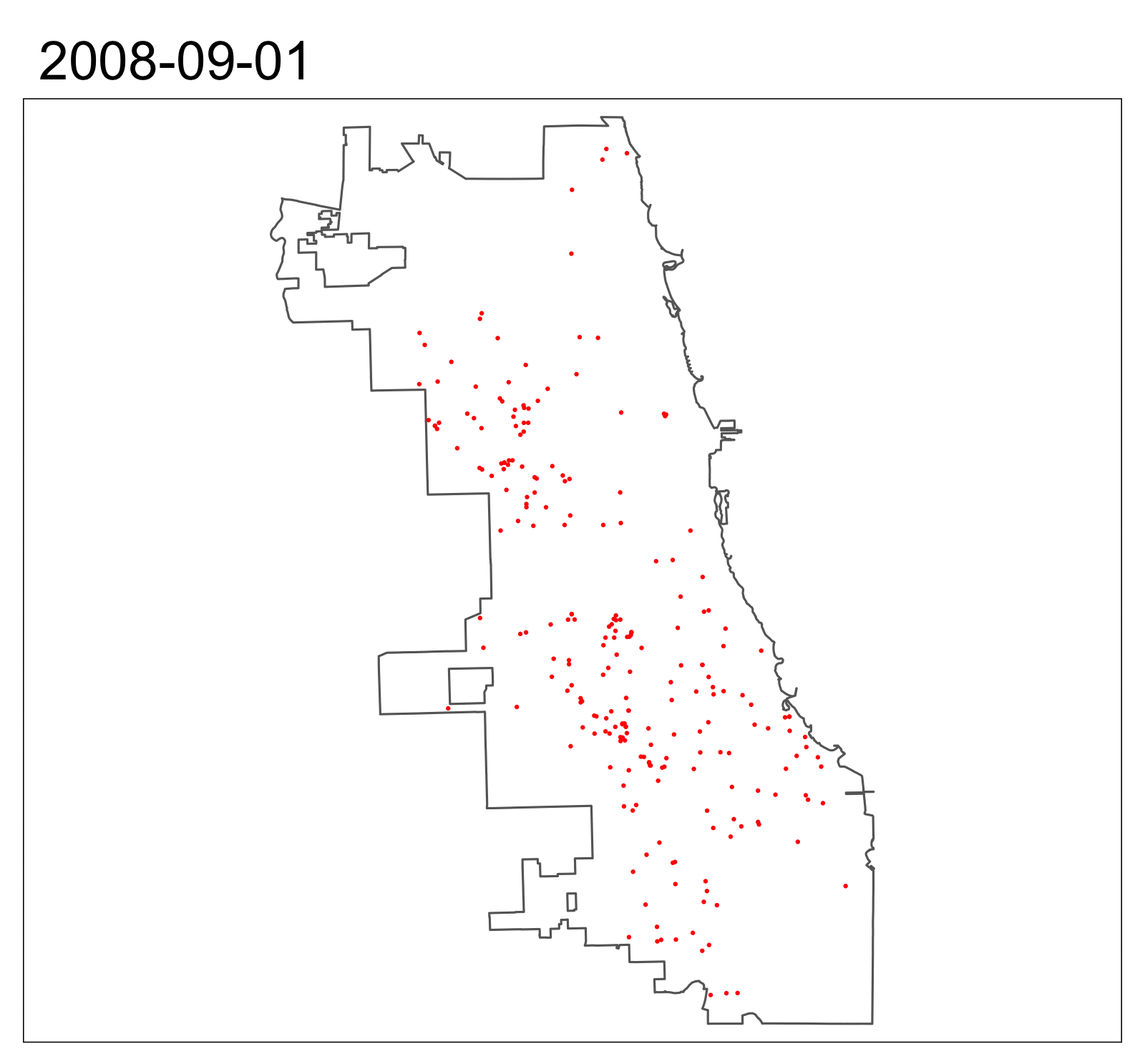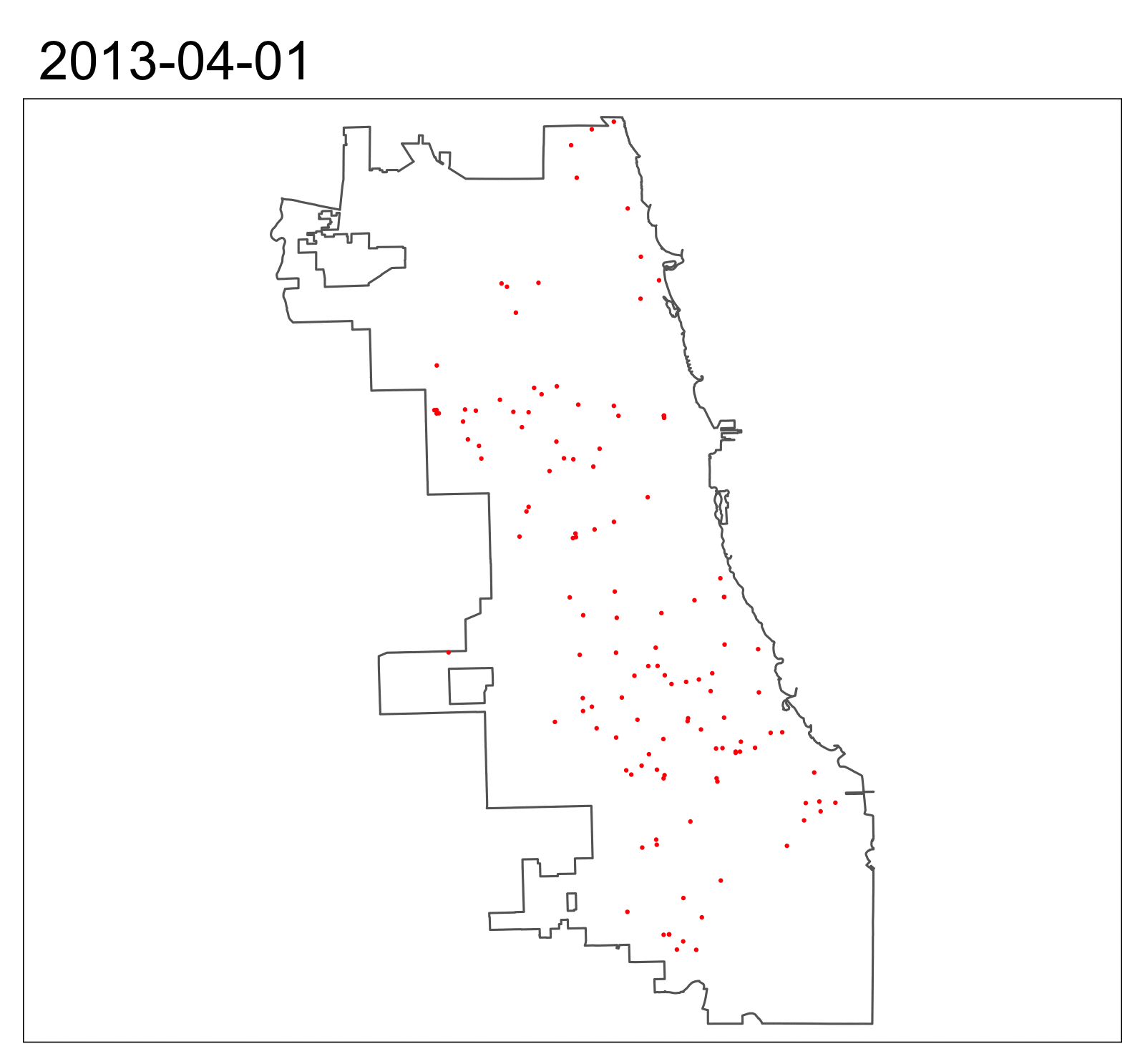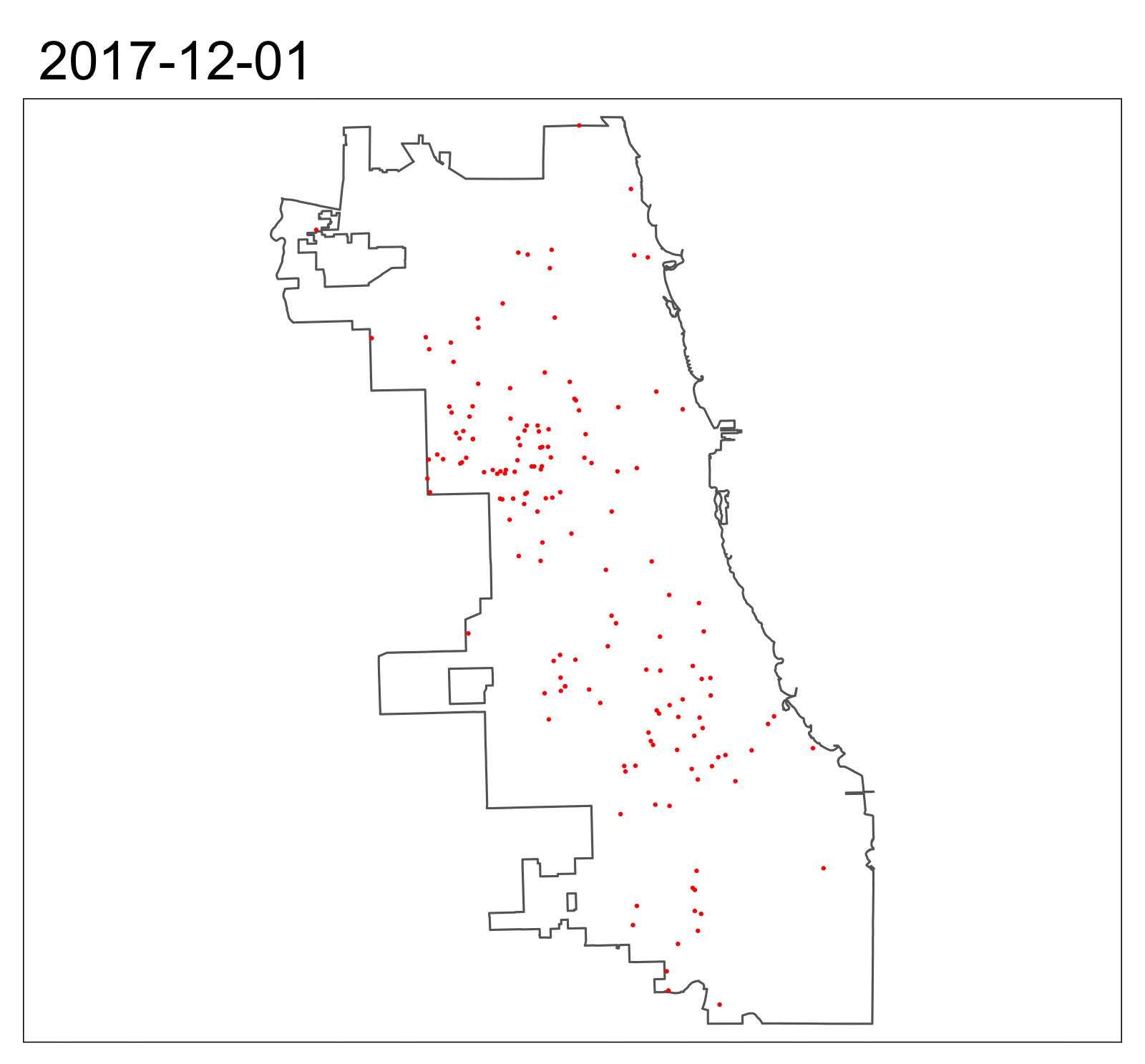
Gunshots, Panel Construction

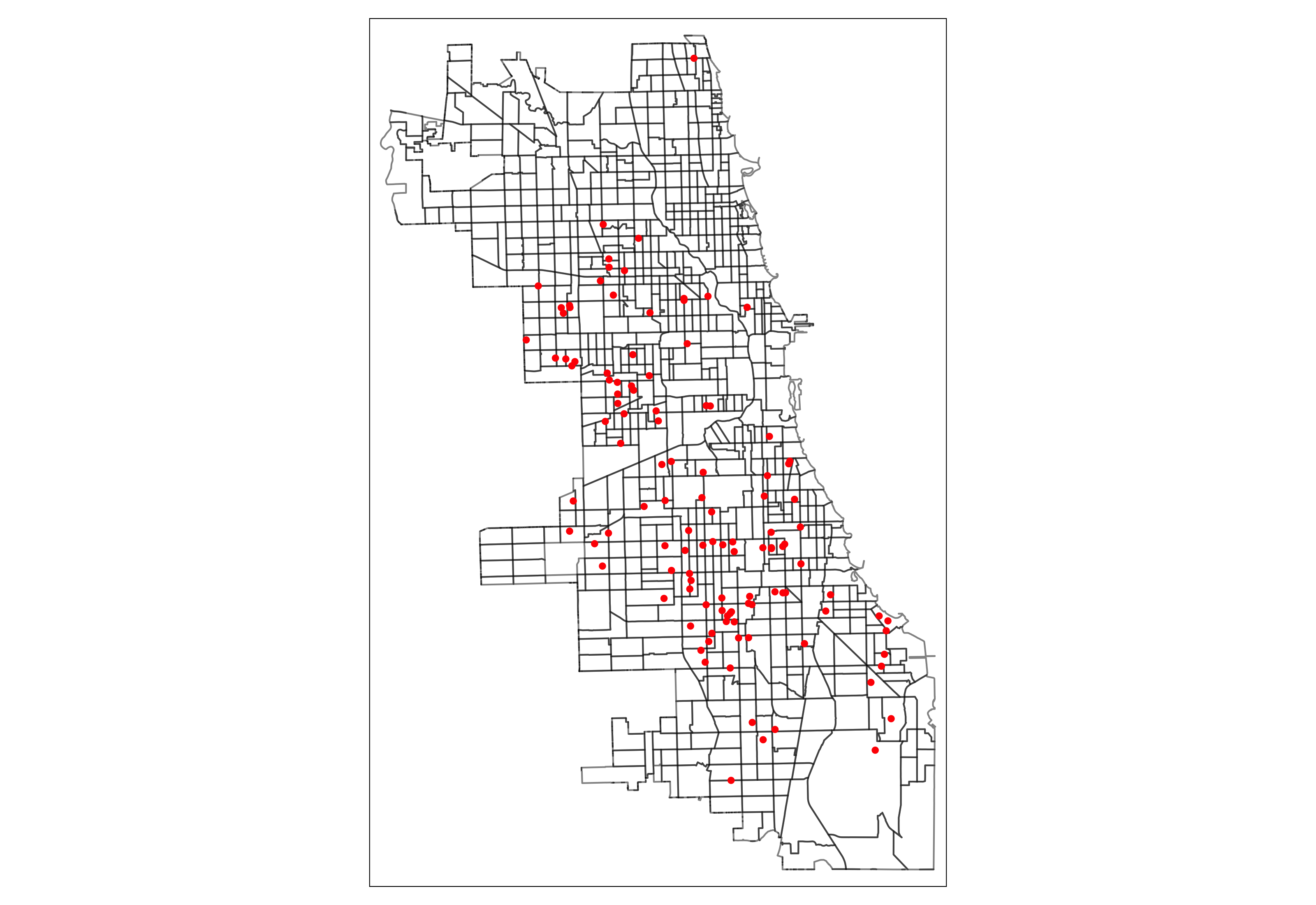
Gunshots, Panel Construction

  • \(N\) tracts
  • \(T\) months

\[ \bm{v} = \begin{pmatrix} v_1^1 & \cdots & \cdots & \cdots & v_1^T \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ \vdots & & v_i^t & & \vdots \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ v_N^1 & \cdots & \cdots & \cdots & v_N^T \end{pmatrix} \]

Turf, Change over Time

Model

Model

Observables

  • \(\mathcal{N} = \left\{1, ..., N \right\}\) – districts
  • \(1, ..., T\) – periods (months)
  • \(r_i\) – the number of residents in territory \(i\)
  • \(v_i^t = x_i^t + y_i^t\)
    • \(y_i^t\) – non-gang related shootings
    • \(x_i^t\) – gang-related shootings

Unobservables

  • \(\mathcal{K} = \left\{1, ..., K \right\}\) – gangs
  • \(\pi : \mathcal{N} \rightarrow \left\{ 0, \mathcal{K} \right\}\) - partition function
    • \(\pi(i) = 0\) indicates the absence of any gang activity.
    • \(\mathcal{N}_k\) – the set of territories controlled by gang \(k\)
    • \(n_k = | \mathcal{K}_k |\) – the number of territories controlled by gang \(k\)
    • \(\mathcal{K}_0\) – the set of unoccupied territories.
    • \(m_k\) – the number of members of gang \(k\)

Varieties of Violence

Non-Gang

  • \(\eta_i\) – the probability a resident commits a shooting
    • independent across districts

Intra-Gang

  • \(\xi_k^t\) – probability a member of gang \(k\) shoots a member of his own gang
  • Assumption 1 (Positivity): \(\mathbb{E} [ \xi_k^t ] > 0\) for all \(k \neq 0\) and \(\xi_0^t = 0\) for all \(t\)
  • Assumption 2 (Independence): \(\mathbb{E} [ \xi_k^t \xi_{\ell}^t ] - \mathbb{E} [ \xi_k^t ] \mathbb{E}[ \xi_{\ell}^t ] = 0\) for all \(k \neq \ell\)

Inter-Gang

  • \(\epsilon_{k, \ell}^t\) – the probability a member of gang \(k\) shoots a member of gang \(\ell\)
  • Assumption 3 (Quasi-symmetry): \(c_{k} \epsilon_{k, \ell}^t = c_{\ell} \epsilon_{\ell, k}^{t}\) with the normalization \(c_1 = 1\). If \(k = 0\) or \(\ell = 0\) then \(\epsilon_{k, \ell}^t = 0\) for all \(t\)
  • Assumption 4 (Independence): \(\mathbb{E} [ \epsilon_{k, \ell}^t \epsilon_{m, n}^t ] - \mathbb{E} [ \epsilon_{k, \ell}^t ] \mathbb{E} [ \epsilon_{m, n}^t ] = 0\) for \(m, n \notin \left\{ k, \ell \right\}\)
  • Probability a member of gang \(\pi(i)\) is operating on territory \(i\) \[ \frac{1}{n_{\pi(i)}} \]

Varieties of Violence

Gang-Related Shootings

\[ \mathbb{E} [ x_i^t ] = \underbrace{ \frac{m_{\pi(i)}}{n_{\pi(i)}} \mathbb{E} [ \xi_{\pi(i)}^t ]}_{ \text{intra-gang} } + \underbrace{\sum_{k \neq \pi(i)} \frac{m_{\pi(i)}}{n_{\pi(i)}} \mathbb{E} [ \epsilon_{k, \pi(i)}^t ]}_{ \text{inter-gang} } \]

Non-Gang Related Shootings

\[ \mathbb{E} [y_i^t] = \eta_i r_i \] \[ \text{Var} [ y_i^t ] = \psi_i = \eta_i (1 - \eta_i) r_i \]

Covariance Structure

Proposition 1: The covariance in shootings between districts \(i\) and \(j\) is \[ a_{ij} = \begin{cases} \sum_{k \neq \pi(i)} \left( \left( \frac{m_{\pi(i)}}{n_{\pi(i)}} \right)^2 \text{Var} [ \epsilon_{k, \pi(i)}^t ] \right) + \left( \frac{m_{\pi(i)}}{n_{\pi(i)}} \right)^2 \text{Var}[ \xi_{\pi(i)}^t ] + \psi_i & \text{if } i = j \\ \color{bcOrange} \sum_{k \neq \pi(i)} \left( \left( \frac{m_{\pi(i)}}{n_{\pi(i)}} \right)^2 \text{Var} [ \epsilon_{k, \pi(i)}^t ] \right) + \left( \frac{m_{\pi(i)}}{n_{\pi(i)}} \right)^2 \text{Var} [ \xi_{\pi(i)}^t ] & \text{if } \pi(i) = \pi(j) \\ \color{bcOrange} \frac{m_{\pi(i)}}{n_{\pi(j)}} \frac{m_{\pi(j)}}{n_{\pi(i)}} \frac{c_{\pi(j)}}{c_{\pi(i)}} \text{Var} [\epsilon_{\pi(i), \pi(j)}^t] & \text{if } \pi(i) \neq \pi(j) \\ 0 & \text{otherwise} \end{cases} \]

Corollary 1 (Block Structure):

  1. If \(\pi(i) = \pi(j) = k\) and \(i \neq j\) then \(a_{ij} = b_{kk}\) constant for all \(i, j\).
  2. If \(\pi(i) = k\) and \(\pi(j) = \ell\) with \(\ell \neq k\) then \(a_{ij} = b_{k \ell}\) constant for all \(i, j\).

Covariance Structure

\[ A_{N \times N} = (a_{ij})_{ \left\{ i,j \in \mathcal{N} \right\} } \]

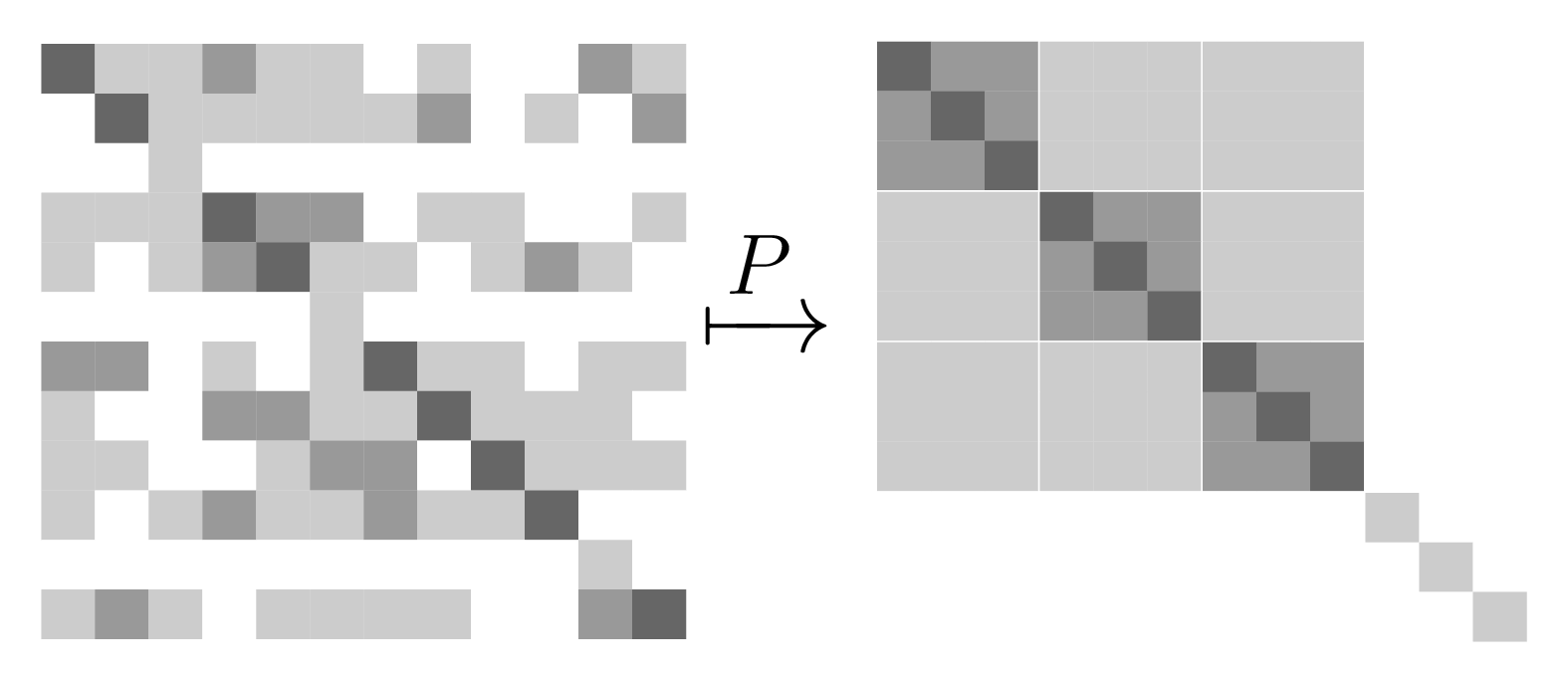
\[ \bar{A} = P A P \]

Covariance Structure and Latent Variables

  • Variance of non-gang shootings \[ \Psi = \text{diag}(\psi_1, \dots \psi_N) \]
  • Gang-related spatial covariance matrix \[ Q = A - \Psi \]
  • Within-gang variance and cross-gang covariances \[ B_{K + 1 \times K + 1} = (b_{k \ell})_{ \left\{ k, \ell \in \mathcal{K} \right\} } \]
  • Binary membership matrix, \(\theta_{ik} = 1\) if \(\pi(i) = k\) and \(0\) otherwise \[ \Theta_{N \times K + 1} = (\theta_{ik})_{\left\{ i \in \mathcal{N}, k \in \mathcal{K} \cup 0 \right\} } \]
  • Stochastic blockmodel (Holland, Laskey, and Leinhardt 1983; Jin 2015; Lei and Rinaldo 2015) \[ Q = \Theta B \Theta^T \]

Example

\[ \Theta = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \]

\[ \color{bcOrange} Q = \Theta B \Theta^T \]

\[ \begin{array}{ccc} ~ & \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} & \begin{pmatrix} 1_{\color{white} 11} & 1_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} \\ 0_{\color{white} 11} & 0_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} \end{pmatrix} \\ \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} & \begin{pmatrix} \color{white} b_{11} & \color{white} b_{12} \\ \color{white} b_{11} & \color{white} b_{12} \\ \color{white} b_{21} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{22} \end{pmatrix} & \begin{pmatrix} \color{white} b_{11} & \color{white} b_{11} & \color{white} b_{12} & \color{white} b_{12} & \color{white} b_{12} \\ \color{white} b_{11} & \color{white} b_{11} & \color{white} b_{12} & \color{white} b_{12} & \color{white} b_{12} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \end{pmatrix} \end{array} \]

Example

\[ \Theta = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \]

\[ \color{bcOrange} Q = \Theta B \Theta^T \]

\[ \begin{array}{ccc} ~ & \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} & \begin{pmatrix} 1_{\color{white} 11} & 1_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} \\ 0_{\color{white} 11} & 0_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} \end{pmatrix} \\ \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} & \begin{pmatrix} \color{bcOrange} b_{11} & \color{black} b_{12} \\ \color{bcOrange} b_{11} & \color{black} b_{12} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \end{pmatrix} & \begin{pmatrix} \color{white} b_{11} & \color{white} b_{11} & \color{white} b_{12} & \color{white} b_{12} & \color{white} b_{12} \\ \color{white} b_{11} & \color{white} b_{11} & \color{white} b_{12} & \color{white} b_{12} & \color{white} b_{12} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \\ \color{white} b_{21} & \color{white} b_{21} & \color{white} b_{22} & \color{white} b_{22} & \color{white} b_{22} \end{pmatrix} \end{array} \]

Example

\[ \Theta = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} \]

\[ \color{bcOrange} Q = \Theta B \Theta^T \]

\[ \begin{array}{ccc} ~ & \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} & \begin{pmatrix} 1_{\color{white} 11} & 1_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} & 0_{\color{white} 11} \\ 0_{\color{white} 11} & 0_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} & 1_{\color{white} 11} \end{pmatrix} \\ \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{pmatrix} & \begin{pmatrix} \color{bcOrange} b_{11} & \color{black} b_{12} \\ \color{bcOrange} b_{11} & \color{black} b_{12} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{bcOrange} b_{22} \end{pmatrix} & \begin{pmatrix} \color{bcOrange} b_{11} & \color{bcOrange} b_{11} & \color{black} b_{12} & \color{black} b_{12} & \color{black} b_{12} \\ \color{bcOrange} b_{11} & \color{bcOrange} b_{11} & \color{black} b_{12} & \color{black} b_{12} & \color{black} b_{12} \\ \color{black} b_{21} & \color{black} b_{21} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{black} b_{21} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} \\ \color{black} b_{21} & \color{black} b_{21} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} & \color{bcOrange} b_{22} \end{pmatrix} \end{array} \]

Estimation

Estimation

Targets

  • Partition function, \(\pi\) (membership matrix: \(\Theta\))
  • Number of groups \(K\)
  • Non-gang territory, \(\mathcal{N}_0\)

Method

  1. Hold \(K\) fixed, estimate partition (\(\color{bcOrange} J = K + 1\))
  2. Cross validate over many trial \(K\) to estimate number of groups

Sample Covariance Matrix Construction

\[ \tilde{a}_{ij} = \frac{1}{N} \sum_{t=1}^T (v_i^t - \bar{v}_i) (v_j^t - \bar{v}_j) \]

\[ \bm{v} = \begin{pmatrix} v_1^1 & \cdots & \cdots & \cdots & v_1^T \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ \vdots & & v_i^t & & \vdots \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ v_N^1 & \cdots & \cdots & \cdots & v_N^T \end{pmatrix} \rightarrow \begin{pmatrix} \tilde{a}_{11} & \cdots & \cdots & \cdots & \tilde{a}_{1N} \\ \vdots & & & & \vdots \\ \vdots & & \tilde{a}_{ij} & & \vdots \\ \vdots & & & & \vdots \\ \tilde{a}_{N1} & \cdots & \cdots & \cdots & \tilde{a}_{NN} \end{pmatrix} = \tilde{A} \]

Estimation Problem

Finite Sample Noise

\[ \tilde{A} = \mathbb{E} [A] + \Phi \]

  • \(\Phi = (\phi_{ij})_{ \left\{ i, j \in \mathcal{N} \right\} }\)
  • \(\mathbb{E} [ \phi_{ij} ] = 0\) for all \(i, j\)

\[\begin{align*} Q - \text{diag}(Q) &= \mathbb{E}[A] - \text{diag}(\mathbb{E}[A]) \\ &= \tilde{A} - \Phi - \text{diag}(\mathbb{E}[A]) \\ \Phi - \text{diag}(\Phi) &= \left( \tilde{A} - \text{diag}(\tilde{A}) \right) - \left( Q - \text{diag}(Q) \right) \end{align*}\]

Moment Estimator

\[\begin{equation} \left( \hat{\Theta}, \hat{B} \right) = \argmin_{B \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J}} \lVert \Phi - \text{diag}(\Phi) \rVert_F \end{equation}\]

Eigenstructure of \(Q\) (Lei and Rinaldo (2015))

  • \(\Delta = \text{diag}(\sqrt{n_1}, \dots, \sqrt{n_{J}})\)

\[\begin{align*} Q &= \Theta B \Theta^T \\ &= \Theta \Delta^{-1} \Delta B \Delta \Delta^{-1} \Theta^T \\ &= \Theta \Delta^{-1} Z \Lambda Z^T \Delta^{-1} \Theta^T \\ &= \Theta X \Lambda X^T \Theta^T \\ U D U^T &= \Theta X \Lambda X^T \Theta^T \end{align*}\]

  • \(\Lambda = \text{diag}(\lambda_1, ..., \lambda_{J})\) eigenvalues of \(\Delta B \Delta\)
    • \(Z_{N \times J}\) associated eigenvectors
  • \(X = \Delta^{-1} Z\)
  • \(U = \Theta X\) orthonormal \(\implies U D U^T\) is eigendecomposition of \(Q\)
    • \(J\) independent rows \(\implies J\) non-zero eigenvalues

Spectral Clustering: Relate eigenvectors of empirical covariance matrix \(\tilde{A}\) to those of \(Q\)

\[ \tilde{A} - \text{diag}(\tilde{A}) = \tilde{U} \tilde{\Lambda} \tilde{U}^T \]

  • \(\tilde{\Lambda}_{J \times J}\) – \(J\) leading eigenvalues
  • \(\tilde{U}_{N \times J}\) – associated eigenvectors

Modified Estimation Problem

\[\begin{align*} \left( \hat{\Lambda}, \hat{X}, \hat{\Theta} \right) &= \argmin_{ \Lambda \in \mathbb{D}^{J \times J}, X \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J} } \lVert \Phi - \text{diag}(\Phi) \rVert_F \\ &= \argmin_{ \Lambda \in \mathbb{D}^{J \times J}, X \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J} } \lVert \left( \tilde{A} - \text{diag}(\tilde{A}) \right) - \left( Q - \text{diag}(Q) \right) \rVert_F \\ &= \argmin_{ \Lambda \in \mathbb{D}^{J \times J}, X \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J} } \lVert \tilde{U} \tilde{\Lambda} \tilde{U}^T - \left( \Theta X \Lambda X^T \Theta^T - \text{diag}(Q) \right) \rVert_F \\ &\approx \argmin_{ \Lambda \in \mathbb{D}^{J \times J}, X \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J} } \lVert \color{bcOrange} \tilde{U} \color{black} \tilde{\Lambda} \color{bcOrange} \tilde{U}^T \color{black} - \color{bcOrange} \Theta X \color{black} \Lambda \color{bcOrange} \left( \Theta X \right)^T \color{black} \rVert_F \end{align*}\]

  • Set \(\hat{\Lambda} = \tilde{\Lambda}\)

\[\begin{equation} \label{eq:kmeans} \left( \hat{X}, \hat{\Theta} \right) = \argmin_{ X \in \mathbb{R}^{J \times J}, \Theta \in \mathbb{M}^{N \times J} } \lVert \color{bcOrange} \Theta X - \tilde{U} \color{black} \rVert_F \end{equation}\]

  • K-means problem

Inter- and Intra-Gang Conflict Estimates

\[\begin{equation} \label{eq:B} \hat{B} = \hat{X} \hat{\Lambda} \hat{X}^T \end{equation}\]

Non-Gang Territory

  • No covariance with gang territory in expectation,
    • \(\mathbb{E} [ b_{0k} ] = 0\) for all \(k \neq 0\)

Estimator

\[\begin{equation} \label{eq:nc} \min_{ k \in \left\{ 1, ..., J \right\} } \lVert ( \hat{B} - \text{diag}(\hat{B}) )^{(k)} \rVert_2 \end{equation}\]

Number of Groups (Chen and Lei 2018)

  1. For each \(k \in \left\{ 1, ..., \bar{K} \right\}\)…
    • Randomly split districts into folds \(\mathcal{N}_1, \dots, \mathcal{N}_V\).
    • For each fold, estimate \(\hat{\Theta}(v)\) and \(\hat{B}(v)\).
    • For each fold, calculate the predictive loss on \(\tilde{A}^{(v,v)}\), \(L_v(\tilde{A}, \hat{A}(v))\)
    • Average the predictive loss across folds, \(\bar{L}_{k}(\tilde{A})\).
  2. Construct the sequence of changes in predictive loss, \(\delta\). \[ \delta_k = \bar{L}_{k}(\tilde{A}) - \bar{L}_{k+1}(\tilde{A}) \]
  3. Select \(\hat{J}\) at first point in sequence where predictive loss does not decrease \[\begin{equation} \hat{J} = \argmin_{k} \left\{ k \mid \delta_k < 0 \right\}_{k \in \left\{ 1, \dots, \bar{K} \right\} } \end{equation}\]
  • Alternative approach: eigengaps (Ahn and Horenstein 2013)

Details

Uncertainty (Nonparametric Bootstrap)

  1. Sample homicides and non-fatal shootings with replacement
  2. Construct sequence of bootstrapped violence matrices \[ \left\{ \bm{v}_1, \dots, \bm{v}_{B} \right\} \]
  3. Construct accompanying sequence of covariance matrices \[ \left\{ \tilde{A}_1, \dots, \tilde{A}_{B} \right\} \]
  4. Re-estimate \(\hat{J}_B\) and \(\hat{\Theta}_B\) as above
    • For validation, match each \(\hat{\Theta}_B\) to CPD maps by permuting census tract labels to minimize disagreement
  5. Present 95 percent confidence intervals

Results

Results

Number of Gangs

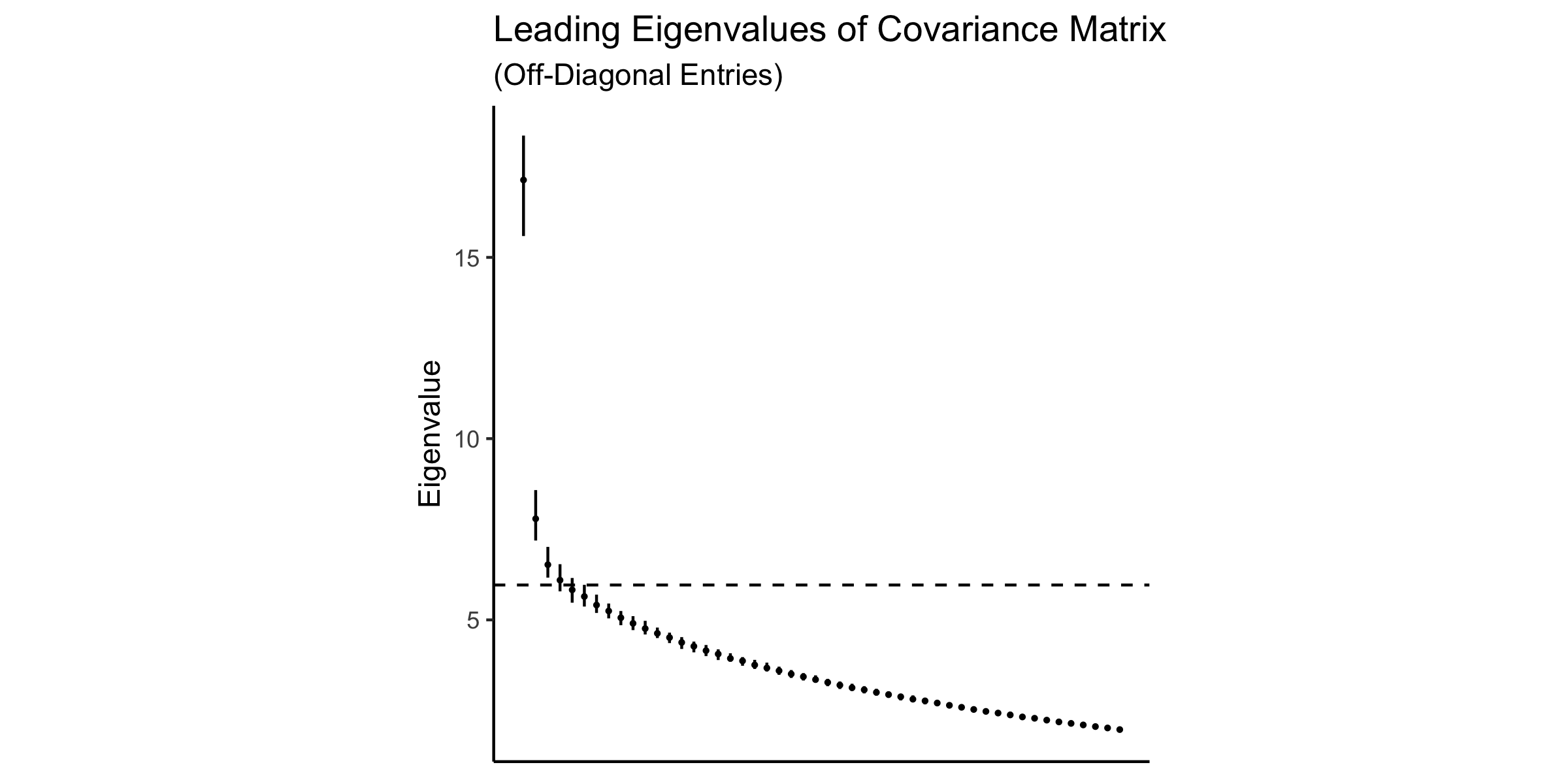
  • 3-4 gangs detected
  • 39 gangs own at least one tract according to CPD, but three largest gangs we detect occupy 57 percent of all gang turf
  • Eigengaps

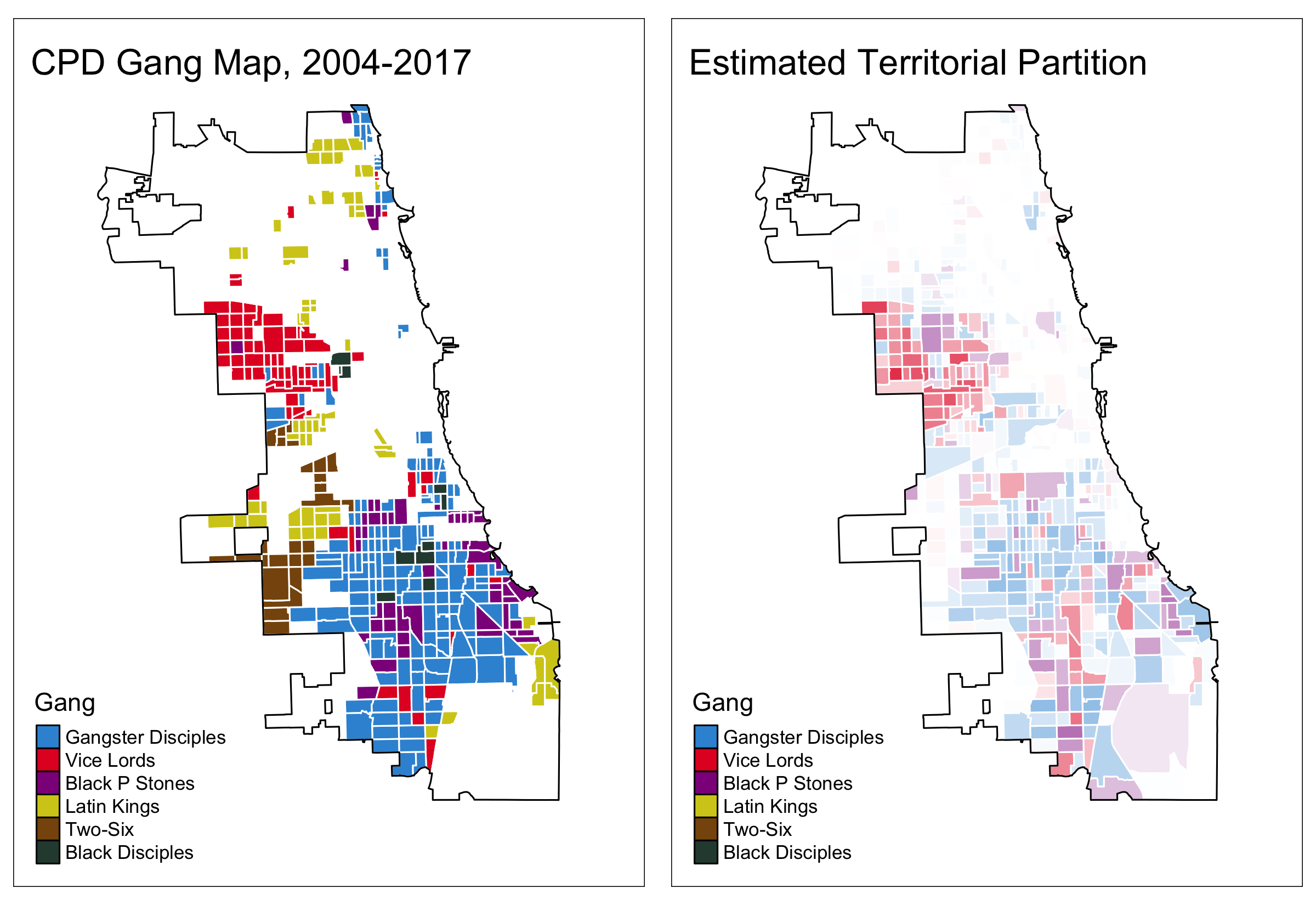
Territorial Partition

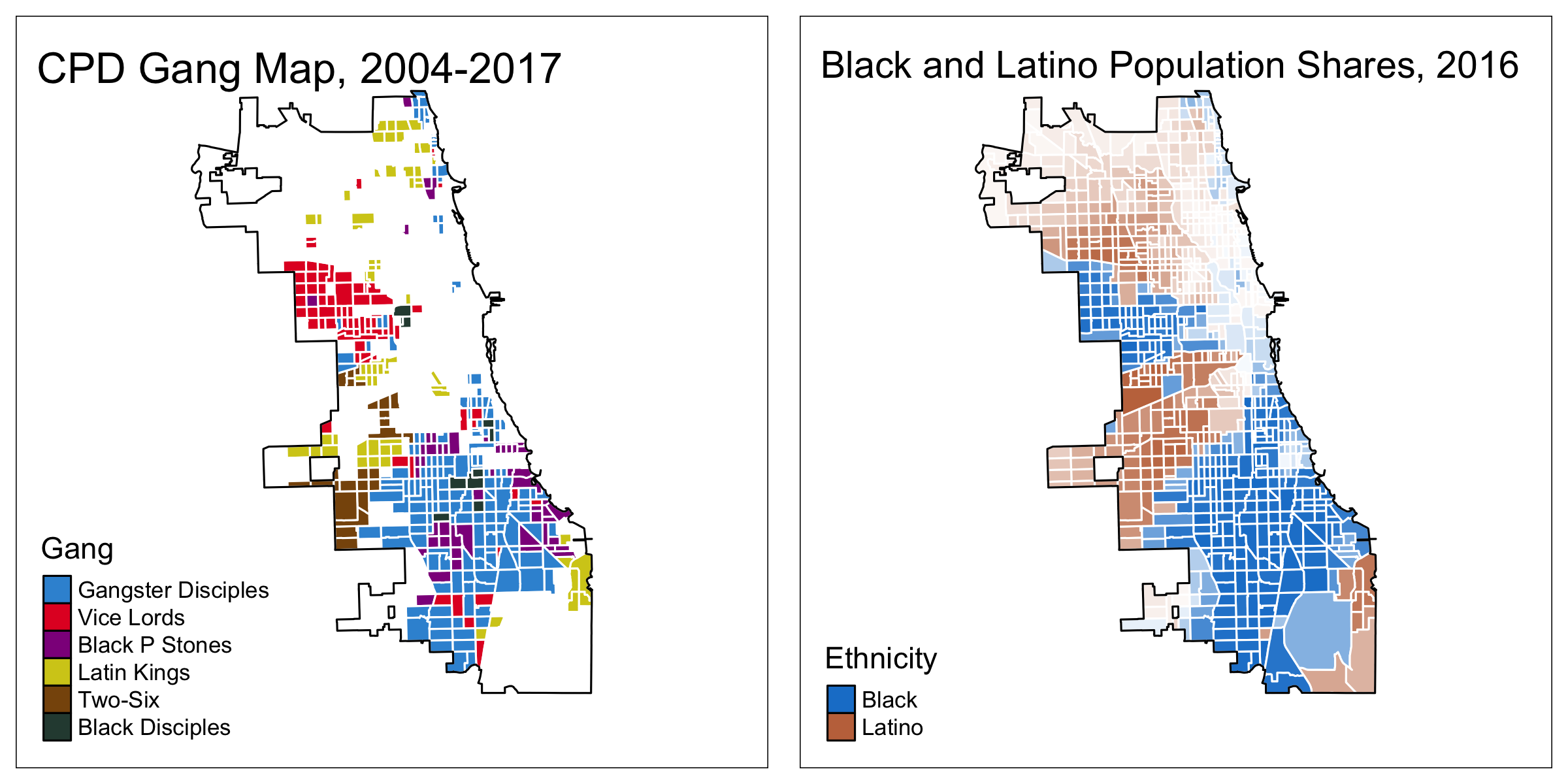
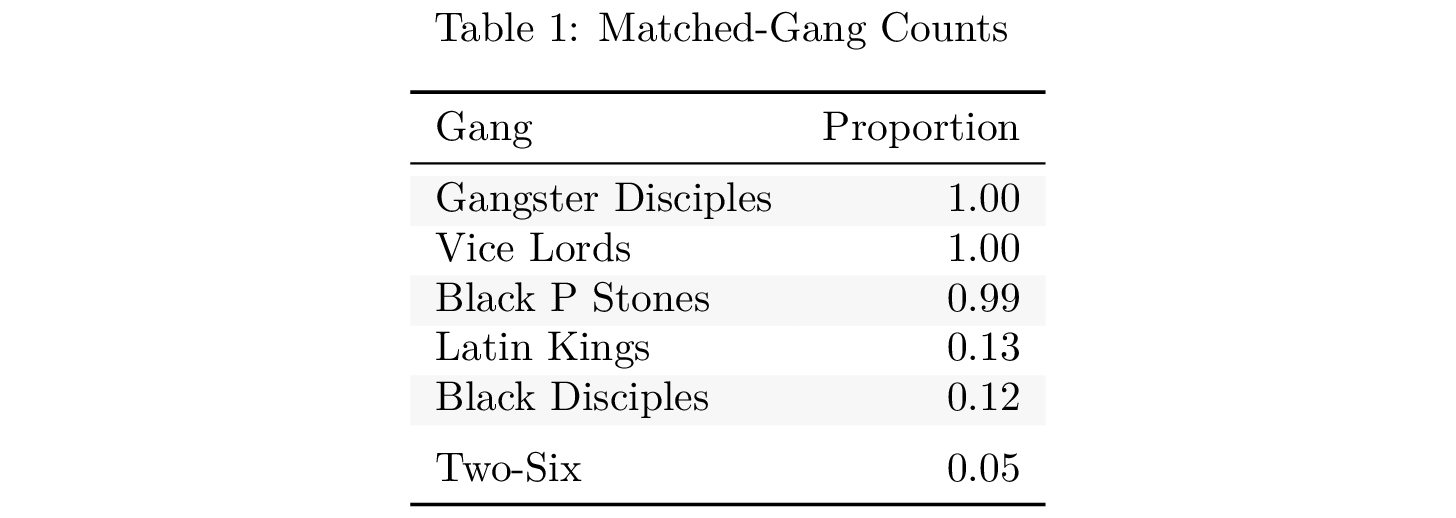
  • Paritition labels matched to those of Gangster Disciples, Vice Lords, and Black P Stones with highest frequency
  • 20-28 percent of census tracts are gang-occupied
  • 56-60 percent of our labels agree with those of CPD
    • Baseline: 35 percent of CPD labels agree with random label permutations
  • Match Frequencies

Empirical Covariances

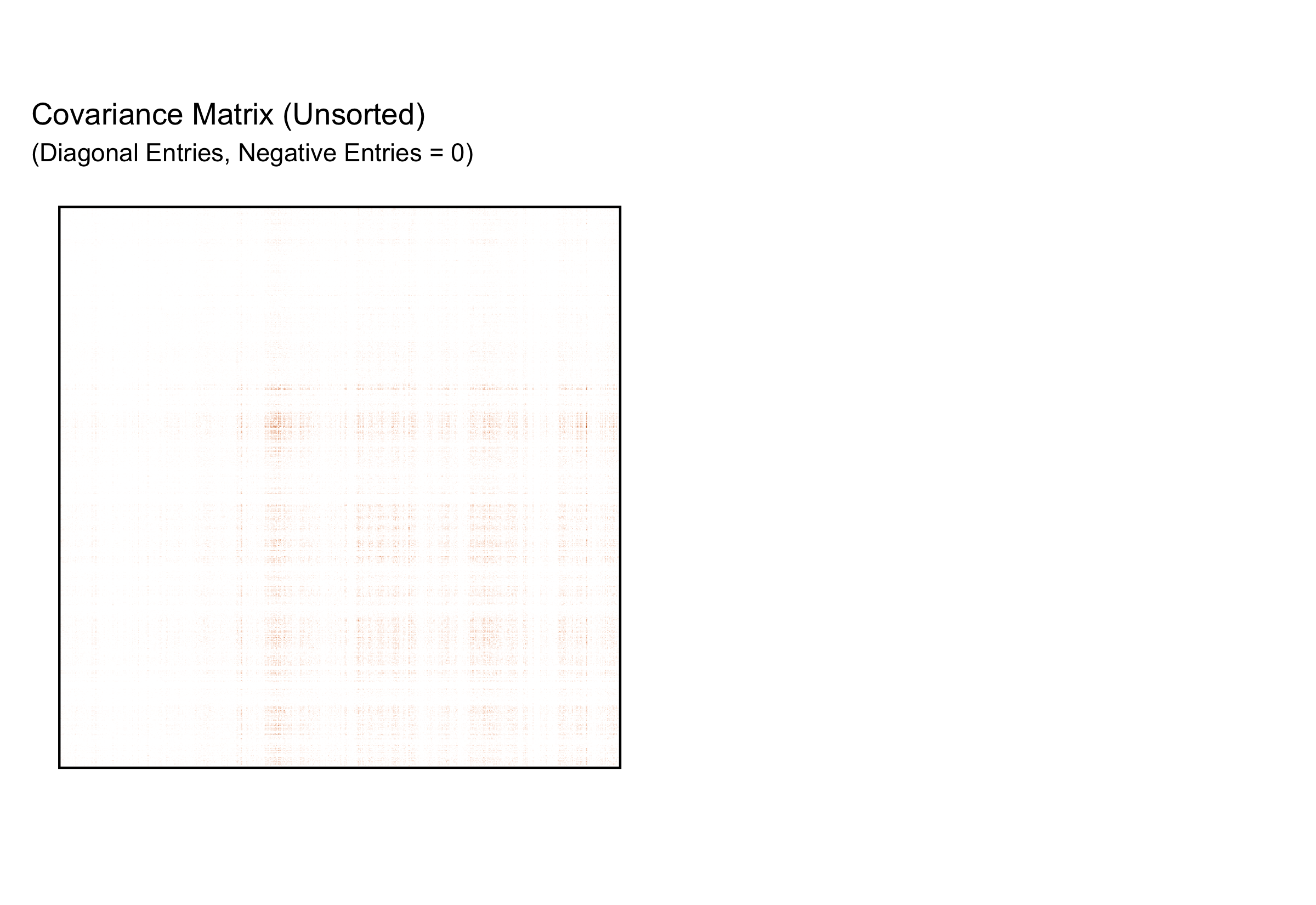
Empirical Covariances

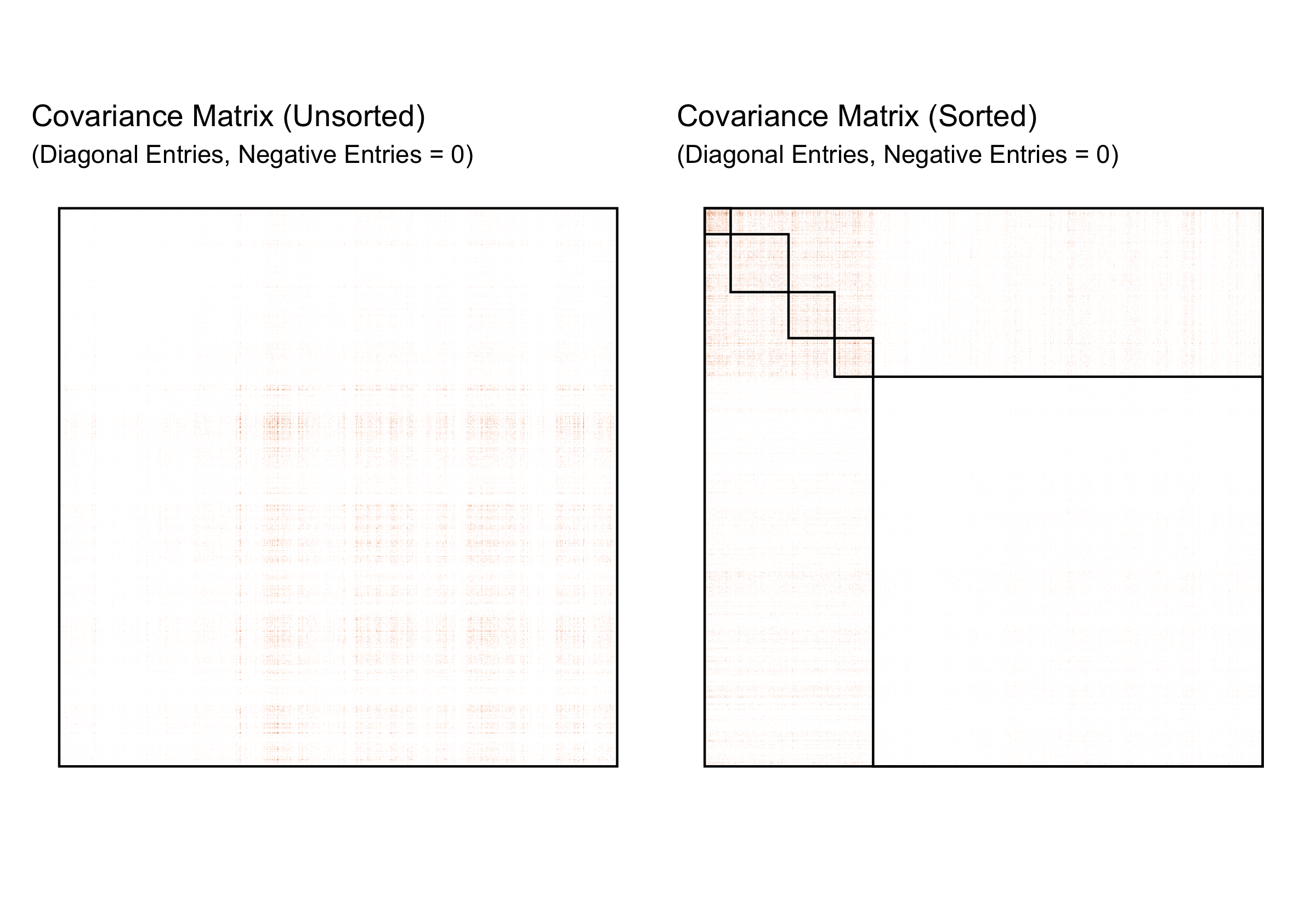
Territorial Partition

Conflict Intensities

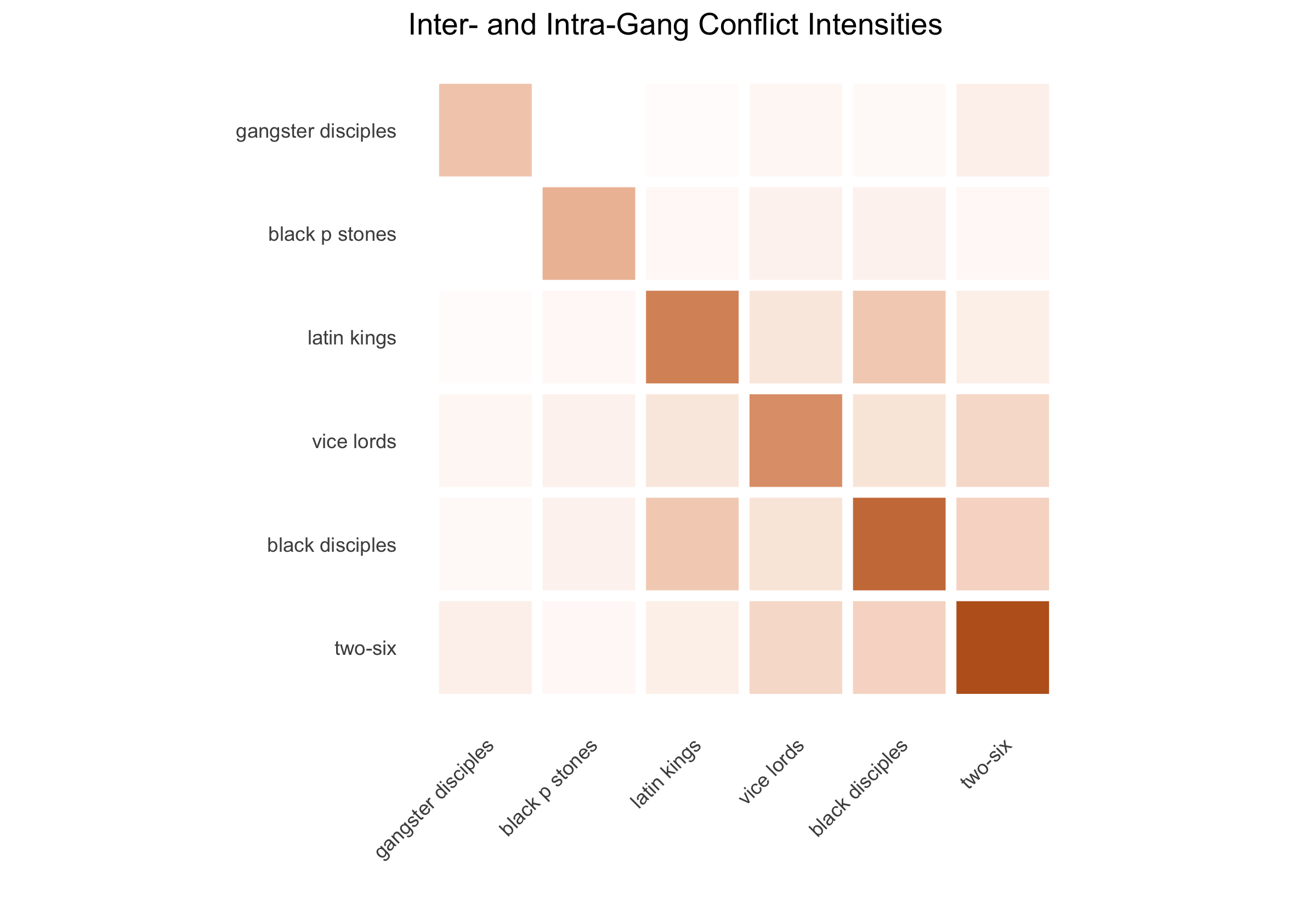
Conflict Intensities

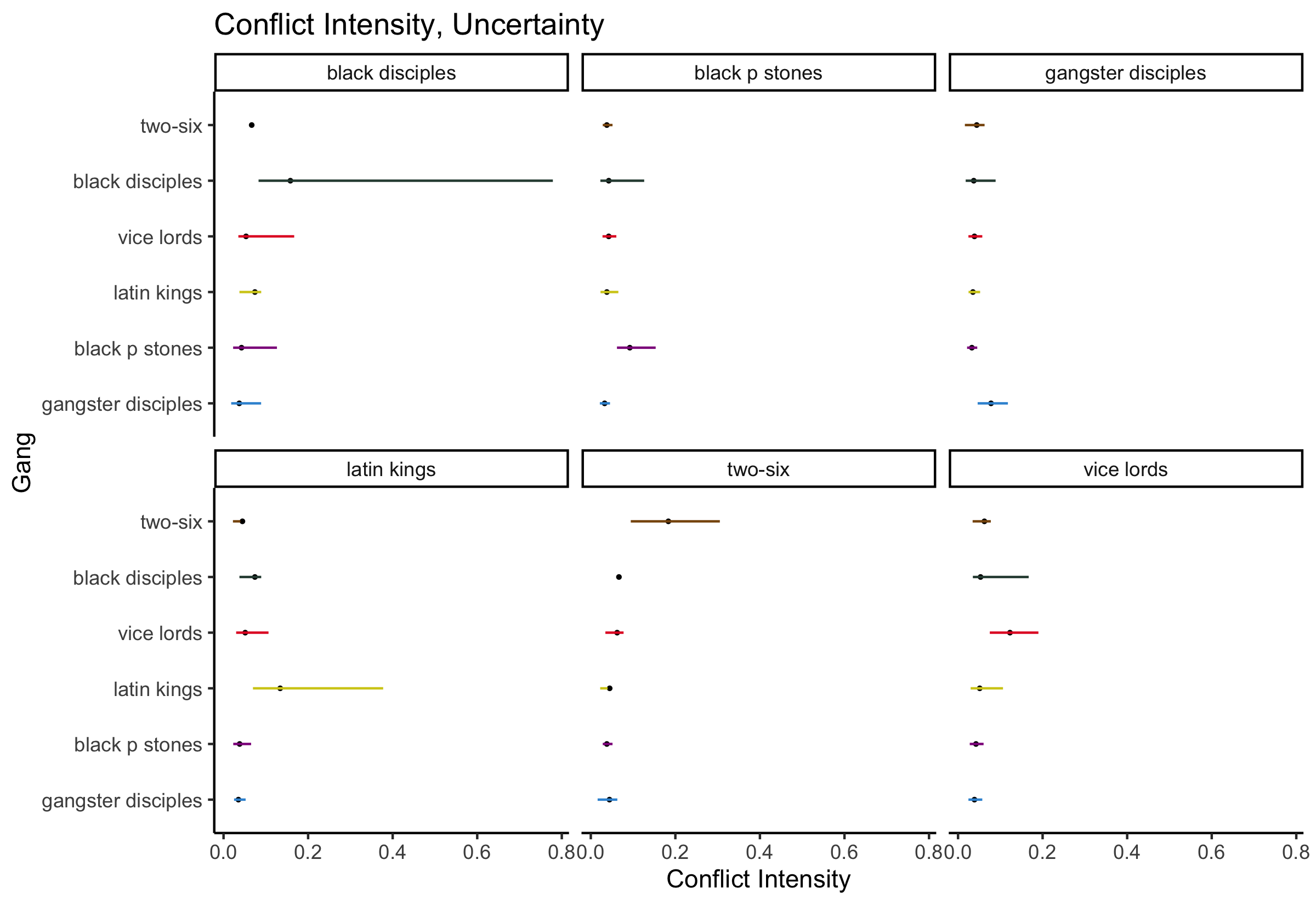
Conclusions

Conclusions

Limitations

  • Collapse dynamic process of border adjustment into static representation (Bruhn 2019)
  • Detects largest gangs in Chicago but is unable to capture richness of gang network

Extensions

  • Extend to other cities
    • Data is available for all large municipalities
  • Build cross section of gang maps across United States and elsewhere(?)
    • Characterize measurement error explicitly
  • Building block for substantive research on gangs, violence, poverty, and policing

Thank You

Table of Contents

Appendix

Territorial Distribution

Back (Data)

Back (TOC)

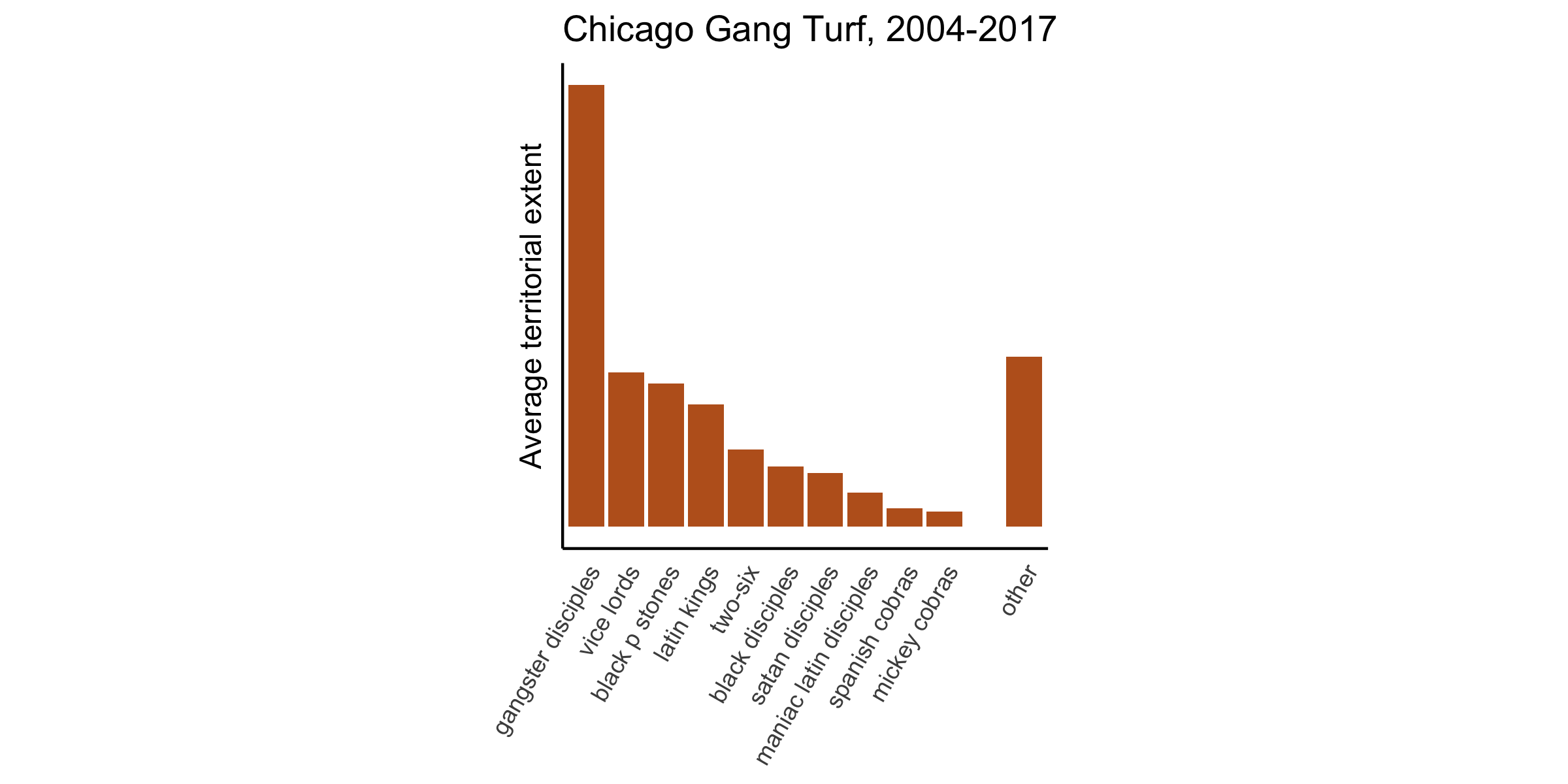
Gang Boundaries and Neighborhood Ethnicity

Back (Data)

Back (TOC)

Number of Groups (I)

  • Rectangular subset of \(\tilde{A}\), \(\tilde{A}^{(-v, v)} = \tilde{A}^{(\mathcal{N}_{-v}, \mathcal{N})}\)
  • Theoretical analogue \[ Q^{(-v, v)} = \Theta^{(-v, v)} B \Theta \]
  • Eigenstructure of \(\left( Q^{(-v, v)} \right)^T Q\) \[\begin{align*} \left( Q^{(-v, v)} \right)^T Q &= \Theta B^T \left( \Theta^{(-v, v)} \right)^T \Theta^{(-v, v)} B \Theta^T \\ &= \Theta B^T \left( \Delta^{(-v, -v)} \right)^2 B \Theta^T . \end{align*}\]
  • Eigendecompose using right singular values of \(Q^{(-v, v)}\) and k-means cluster to produce membership estimates \(\hat{\Theta}(v)\)

Number of Groups (II)

  • Estimate connectivity matrix \[ \hat{B}_{k, \ell} = \begin{cases} \frac{ \sum_{i \in \hat{\mathcal{N}}_{-v, k}, j \in \hat{\mathcal{N}}_{\ell} } \tilde{A}_{ij} }{ \hat{n}_{v, k} \hat{n}_{\ell}} & \text{if } k \neq \ell \\ \frac{ \sum_{i, j \in \hat{\mathcal{N}}_{-v, k}, i \neq j} A_{ij} + \sum_{i \in \hat{\mathcal{N}}_{-v, k}, j \in \hat{\mathcal{N}}_{v, k} } A_{ij} }{ (\hat{n}_{-v, k} - 1) \hat{n}_{-v, k} + \hat{n}_{-v, k} \hat{n}_{v, k} } & \text{if } k = \ell \end{cases} \]
  • Construct implied covariance matrix \[ \hat{A}(v) = \hat{\Theta}(v) \hat{B}(v) \left( \hat{\Theta}(v) \right)^T \]
  • Calculate loss \[ L_v(\tilde{A}, \hat{A}(v)) = \left\lVert \left( \tilde{A}^{(v,v)} - \text{diag}(\tilde{A}^{(v,v)}) \right) - \left( \hat{A}(v)^{(v,v)} - \text{diag}(\hat{A}(v)^{(v,v)}) \right) \right\rVert_F \]

Back (Estimation)

Back (TOC)

Eigengaps

Back (Results)

Back (TOC)

Match Frequencies

Back (Results)

Back (TOC)

Ahn, Seung C., and Alex R. Horenstein. 2013. “Eigenvalue Ratio Test for the Number of Factors.” Econometrica 81 (3): 1203–27.

Blattman, Christopher, Donald P. Green, Daniel Ortega, and Santiago Tobon. 2019. “Hot Spots Interventions at Scale: the Direct and Spillover Effects of Policing and City Services on Crime.”

Brantingham, P. Jeffrey, George E. Tita, Martin B. Short, and Shannon E. Redi. 2012. “The Ecology of Gang Territorial Boundaries.” Criminology 50 (3): 851–85.

Bruhn, Jesse. 2019. “The Geography of Gang Violence.”

Bueno De Mesquita, Ethan. 2018. “Territorial Conflict over Endogenous Rents.” Journal of Politics.

Chen, Kehui, and Jing Lei. 2018. “Network Cross-Validation for Determining the Number of Communities in Network Data.” Journal of the American Statistical Association 113 (521): 241–51.

Decker, Scott H. 1996. “Collective and normative features of gang violence.” Justice Quarterly 13 (2): 243–64.

Holland, Paul W., Kathryn Blackmond Laskey, and Samuel Leinhardt. 1983. “Stochastic blockmodels: First steps.” Social Networks 5 (2): 109–37.

Howell, James C, and Elizabeth Griffiths. 2018. Gangs in America’s communities. Sage Publications.

Jin, Jiashun. 2015. “Fast Community Detection by SCORE.” The Annals of Statistics 43 (1): 57–89.

Lei, Jing, and Alessandro Rinaldo. 2015. “Consistency of Spectral Clustering in Stochastic Block Models.” The Annals of Statistics 43 (1): 215–37.

Levitt, Steven D, and Sudhir Alladi Venkatesh. 2000. “An economic analysis of a drug-selling gang’s finances.” Quarterly Journal of Economics, 755–89.

Luxburg, Ulrike von. 2007. “A tutorial on spectral clustering.” Statistics and Computing 17 (4): 395–416.

Melnikov, Nikita, Carlos Schmidt-Padilla, and Maria Micaela Sviatschi. 2019. “Gangs, Labor Mobility, and Development.”

National Drug Intelligence Center. 2007. “Chicago High Intensity Drug Trafficking Area Drug Market Analysis.” U.S. Department of Justice.

Papachristos, Andrew V. 2009. “Murder by Structure: Dominance Relations and the Social Structure of Gang Homicide.” American Journal of Sociology 115 (1): 74–128.

Papachristos, Andrew V., David M. Hureau, and Anthony A. Braga. 2013. “The Corner and the Crew: The Influence of Geography and Social Networks on Gang Violence.” American Sociological Review 78 (3): 417–47.

Sanchez-Jankowski, Martin. 1991. Islands in the street: Gangs and American urban society.

Signoret, Patrick. 2020. “Mapping Criminal Organizations to Study Subnational Conflict and Politics.”

Sobrino, Fernanda. 2019. “Mexican Cartel Wars: Fighting for the U.S. Opioid Market,” 1–61.

Thrasher, Frederic Milton. 1927. The gang: A study of 1,313 gangs in Chicago. Chicago IL: University of Chicago Press.

Trebbi, Francesco, and Eric Weese. 2019. “Insurgency and Small Wars: Estimation of Unobserved Coalition Structures.” Econometrica 87 (2): 463–96.

Vargas, Robert. 2016. Wounded city: Violent turf wars in a Chicago barrio. Oxford University Press.

Venkatesh, Sudhir Alladi, and Steven D. Levitt. 2000. “"Are we a family or a business?" History and disjuncture in the urban American street gang.”